[科普中国]-独立

独立在数学中应用广泛，包括线性代数中的向量独立、概率论中的独立、公理系统的独立等。

线性代数中的向量独立线性代数中的向量独立（线性无关），即两个向量不成比例，不可互相表示，没有多余。

联系：生活中的独立，独立的人，即人的独一无二，不可被替代；模块独立：即各个模块之间功能独立，（功能不重复，且不能互相的替代）等等。

概率论中的独立要有两随机事件 A、B 。 A、B 发生的概率分别为 P(A) 和 P(B) ， AB 事件同时发生的概率为 P(AB) 若 P(A)×P(B)=P(AB) ，则 A 与 B 相互独立。事件 A 发生的概率不影响事件 B 发生的概率，反应的是概率运算上的关系。

0≤P(A)≤1

0≤P(B)≤1

0≤P(AB)≤1

公理系统的独立性公理系统的独立性是公理系统一般要求具备的一种性质，在含且仅含 A,A1,A2,...,An条公理的系统中，所谓公理 A 对公理A1,A2,...,An是独立的，系指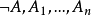是相容的，所谓公理系统是独立的，系指公理中任一条公理与其他的公理相互独立，不独立的公理系统含有多余公理，可从其中删除多余的公理来简化使它成为独立的系统。1

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学