[科普中国]-正方向

正方向是人们规定的一个方向，与正方向相反的是负方向。在数轴中，它是三要素之一；在坐标系中，它也是不可或缺的一部分。引入“正方向”的概念的目的是更好地分析和表示问题。

数轴中的正方向在数学中，人们用画图的方式把数轴“直观化”。通过用一条直线上的点表示数，这条直线叫做数轴。

它满足三个条件：1

（1）在直线上任取一个点表示数0，这个点叫做原点；

（2）通常规定直线上从原点向右（或向上）为正方向，从原点向左（或下）是负方向；

（3）选取适当的长度为单位长度，直线上从原点向右，每隔一个单位长度取一个点，依次表示 ；从原点向左，用类似的方法依次表示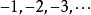

正方向的力量“数轴，通常规定向右为正方向，因此，在数轴上右边的数总比左边的数大。”

“在数轴上明确方向很重要，当规定向右为正方向时，在数轴上越往右，表示的数越大；越往左表示的数就越小。”

“两个数在数轴上的左右位置即决定了两个数的大小。故此，数轴上的方向很重要，方向即决定了数的大小。”

“明确了方向后，还要确定原点。当规定原点即0的位置后，才能确定了正负与负数的分界点。”

“原点0右边的点表示正数；原点0左边的点表示负数。”

“从原点起往右，离开原点的距离的长短，决定了这个正数的数值的大小。同是两个正数，离开原点的距离较长的正数较大，离开原点距离较短的正数较小。”

“从原点起往左则恰好相反，离开原点的距离越远，表示的数越小。同是两个负数，离开原点的距离较短的数较大；离开原点的距原较长的数教小。”

“由此可见，方向很重要，明确方向后，及时找准起点同样重要。只有明确了方向，找准的起点才能更加准确的知道这个数到底有多大。”2

空间直角坐标系中的正方向为了确定空间中任意一点的位置，需要在空间中引进坐标系，最常用的坐标系是空间直角坐标系。

如图，OBCD-D′A′B′C′是单位正方体，以A为原点，分别以OD，OA′，OB的方向为正方向，建立三条数轴x轴，y轴，z轴，这时建立了一个空间直角坐标系O-xyz， 如下图

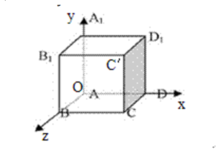
1）O叫做坐标原点；

2）x 轴，y轴，z轴叫做坐标轴；

3）过每两个坐标轴的平面叫做坐标平面；

4）x轴和y轴的方向即为定义的正方向
**右手表示法：**令右手大拇指、食指和中指相互垂直时，可能形成的位置。大拇指指向为x轴正方向，食指指向为y轴正向，中指指向则为z轴正向，这样也可以决定三轴间的相位置。

**任意点坐标表示：**空间一点M的坐标可以用有序实数组（x，y，z）来表示，有序实数组（x，y，z）叫做点M在此空间直角坐标系中的坐标，记作M（x，y，z）（x叫做点M的横坐标，y叫做点M的纵坐标，z叫做点M的竖坐标）。3

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学