[科普中国]-高斯-赛德尔迭代

高斯-赛德尔迭代（Gauss–Seidel method）是数值线性代数中的一个迭代法，可用来求出线性方程组解的近似值。该方法以卡尔·弗里德里希·高斯和路德维希·赛德尔命名。

同雅可比法一样，高斯-赛德尔迭代是基于矩阵分解原理。

发展在数值线性代数中，Gauss-Seidel方法也称为Liebmann方法或连续位移方法，是用于求解线性方程组的迭代方法。 它以德国数学家卡尔·弗里德里希·高斯（Carl Friedrich Gauss）和菲利普·路德维希·冯·塞德尔（Philipp Ludwig von Seidel）命名，与雅可比方法相似。

虽然它可以应用于对角线上具有非零元素的任何矩阵，但如果矩阵是对角线主导的或对称的和正定的则只能保证收敛。 在1823年，只在高斯给他的学生Gerling的私人信中提到。1874年之前没有由塞德尔自行出版。

简介高斯-赛德尔迭代法是解线性方程组的常用迭代法之一，设线性方程组为

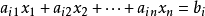
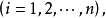
高斯-赛德尔迭代法的迭代公式为

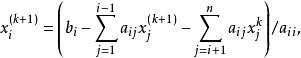
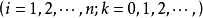
当然，此处假定 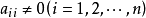，在很多情况下，它比简单迭代法收敛快，它和简单迭代法的不同点在于计算 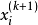时，利用了刚刚迭代出的

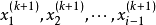的值，当系数矩阵 A 严格对角占优或对称正定时，高斯-赛德尔迭代法必收敛。1

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学