向量值积分,普通(数值的)积分在向量值上的推广。在分析数学的各分支中,因不同的要求,需要种种或是向量值函数的积分或是关于向量值测度的积分。向量值函数的积分有黎曼-斯蒂尔杰斯型积分和勒贝格型积分。
概念黎曼-斯蒂尔杰斯型积分常用的一种向量值积分。如果ƒ(t)是定义在[α,b]上,但取“值”于拓扑线性空间L的函数,则称ƒ(t)是[α,b]上向量值函数。设ƒ(t)和g(t)分别是[α,b]上向量值和数值函数。任取[α,b]上分点组D: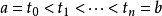 ,作和式
,作和式
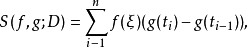 其中
其中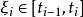 。令
。令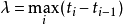 ,如果极限
,如果极限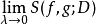 存在,则称ƒ关于g在[α,b]上R-S可积,又称是ƒ关于g的黎曼-斯蒂尔杰斯积分,简称R-S积分,记为
存在,则称ƒ关于g在[α,b]上R-S可积,又称是ƒ关于g的黎曼-斯蒂尔杰斯积分,简称R-S积分,记为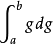 。类似地,也可以引入
。类似地,也可以引入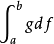 。向量值R-S积分有许多类似于数值函数的R-S积分的性质。特别,有分部积分公式:如果
。向量值R-S积分有许多类似于数值函数的R-S积分的性质。特别,有分部积分公式:如果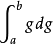 ,
,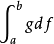 中有一个存在,则另一个必存在,且
中有一个存在,则另一个必存在,且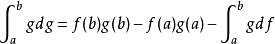 。
。
下面几种向量值积分都属于勒贝格型的。
向量值测度和积分设(x,φ)是可测空间,如果E是定义在φ上取值于巴拿赫空间 B的满足下列条件的向量值集函数:①E(═)=0(═是空集);②可列可加性,对φ中任何一列互不相交的集{Ai},
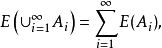
则称E 是φ上向量值测度。例如,如果(x,φ,μ)是全σ有限测度空间,ƒ是x上取值于巴拿赫空间B的博赫纳可积函数,对任何A∈φ,定义
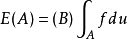
则E便是φ上取值于B的向量值测度。特别,当B是某个巴拿赫空间(或希尔伯特空间)上的有界线性算子全体按算子范数所成的巴拿赫空间时,就称E为φ上的算子值测度(见谱论、谱算子)。此外,和数值测度一样,也可引入一个向量值测度关于另一个数值测度绝对连续的概念。但一般说来没有拉东-尼科迪姆定理。但如果空间B或是自反,或是希尔伯特空间,或B的共轭空间B是可分的,这时就有拉东-尼科迪姆定理。1
测度论测度论是研究一般集合上的测度和积分的理论。它是勒贝格测度和勒贝格积分理论的进一步抽象和发展,又称为抽象测度论或抽象积分论,是现代分析数学中重要工具之一。 测度理论是实变函数论的基础。
若尔当(Jordan,M.E.C.)于1892年在R中发展了佩亚诺可测集的概念。原来定义外测度时,要用多边形去覆盖点集,他规范为用有限个开区间去覆盖,其余不变。若尔当的改进使测度概念前进了一大步,蕴涵了勒贝格测度的萌芽,但仍有明显的缺点。主要是它仍只具有有限可加性,从而导致有些简单的点集也不可测。例如,令A=[0,1]∩Q,则A的若尔当内测度为0,而外测度为1,因而A在若尔当意义下不可测。总之,若尔当测度只适合于黎曼积分的需要。波莱尔(Borel,(F.-É.-J.-)É.)于1898年,先由开集经过可列并与余的运算导致一类集,即所谓波莱尔集类。再对每个有界波莱尔集对应一个实数,即波莱尔测度,并使得这种测度具有可列可加性。波莱尔的这种思想对测度理论做出了重大贡献,成为近代测度论中用公理方式引出σ代数概念的起源,并为勒贝格(Lebesgue,H.L.)的工作开辟了道路.波莱尔的学生勒贝格在前人工作的基础上,于1902年以更一般的形式建立起比较完善的测度理论.他在定义点集测度的方法上,容许可列覆盖,使所建立的测度具有可列可加性,并且相当广泛的一类点集的测度有了定义。勒贝格测度是现代抽象测度的起源,在它的基础上建立的勒贝格积分,是现代分析中应用最广和意义重大的积分。卡拉西奥多里(Carathéodory,C.)于1914年发展了外测度理论,对测度进行了公理化研究,并给出了测度扩张的典型方法,成为近代测度论的基础.拉东(Radon,J.)、萨克斯(Saks,S.)、弗雷歇(Fréchet,M.-R.)以及另外一些人考虑了一般集合上的测度以及测度空间的乘积,并建立了一般可测集上积分的理论。
一般集合上的测度和积分理论是最广泛的测度理论,但为适应各方面的需要,还出现了其他种种特殊的测度和积分.例如,20世纪30年代初,伴随着人们对取值于巴拿赫空间的函数性质特别是可微性和可积性的研究,出现了有关向量值测度的一些工作。1960年以后,向量值测度理论得到蓬勃发展,并逐渐趋于完善。又如,19世纪建立的傅里叶分析理论,对于应用数学而言,当时已是令人满意的数学工具,但由于黎曼积分的局限性,对于函数与展开式之间的关系,直到勒贝格积分理论确立之后才有深刻的揭示.勒贝格积分的出现对于傅里叶展开的研究显然促进了一大步,但依旧显示出了它的局限性。研究拓扑群上的测度是建立群上傅里叶分析的基本问题之一,这个问题自1930年以来,经过哈尔(Haar,A.)、韦伊(Weil,A.)和盖尔范德(Гельфанд,И.М.)等人的工作而趋于完善。再如,20世纪初测度论的建立,使得人们对R中的子集关于n维勒贝格测度的性质有了很好的了解。但在处理与R中低维点集有关的数学问题时遇到了困难。在这种背景下,20世纪20年代出现了几何测度论,它是研究高维空间中低维点集的测度及低维点集上积分的理论。
测度概念与积分概念紧密相关。每一种测度理论的推广都可导致一种积分理论的推广。测度理论不仅是积分理论的基础,而且在现代分析以及概率论等许多数学领域中也有着广泛的应用。
可测空间测度的定义域,测度论中的基本概念。设F是基本空间Ω上的σ代数,称(Ω,F)为可测空间,而称F中的元素A是(Ω,F)中的可测集,也称为Ω中的F可测集,简称可测集。例如,当F是R中的波莱尔集类B时,(R,B)称为波莱尔可测空间。当F是R中的勒贝格可测集类L时,(R,L)称为勒贝格可测空间。可测空间是测度的定义域,在一个可测空间上可以定义不止一种测度。2
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国