[科普中国]-电路变换

电路变换是简化电路计算的一种手段。它是在满足某种条件下，把一个给定的电路中的一部分改变成一个不但连接方式（拓扑结构）不同，而且所含元件的参数数值也不同的新电路。

概念电路变换的连接方式多半比较简单，即使不简单，也能为计算提供一定的方便。最常见到的电路变换是等效变换。这是一种能保证电路的非变换部分中的电压、电流在变换中维持不变的变换。

已经证明，要保证非变换部分中的电压、电流维持不变，变换成的新电路部分必须是变换部分的等效电路，亦即前者与后者应具有相同的外特性。所以，实现这种变换的关键是求出电路变换部分的等效电路。求等效电路的步骤是：首先，根据电路变换部分的电路图用适当的方法写出该部分的外特性方程；然后，根据求得的外特性方程确定等效电路的连接方式（拓扑结构）和相应的元件参数。

把电路内一个由电阻元件连接成的多射线星形变换成一个多角形是这类变换中的一个较为典型的实例。按上述步骤完成这个变换应首先写出多射线星形的外特性方程。

在电路计算中，把几个串联（或并联）的同类元件合并成一个元件是最简单的等效变换。戴维南定理和诺顿定理中的等效替换，以及电源模型间的互换也都是等效变换。虽然替代定理中所进行的替代是根据外特性曲线上的一点相同，而不是整个曲线相同，但因一点相同仍含有等效的意思，故可看成是一种特殊的等效变换。

含受控源电路变换控制量解法初探随着有源元件的广泛使用，含受控源电路的分析也显得越来越重要。在含受控源的电路中，各支路的响应除了受到网络拓朴约束外，又增加了新的约束，因而使得分析计算增加了难度。在用等效变换的方法化简含受控源的电路时，一般认为，受控源可以当作独立源一样参与变换，而控制量则不能变换掉。这就使得等效变换的思路受到了限制，影响了电路的化简。然而，分析表明，控制量是可以进行变换的。

众所周知，一个电路中各部分的电流、电压都要受到基尔霍夫定律、欧姆定律的约束，作为控制量的电流或电压自然也不例外。这就意味着，作为控制量的某个电流或电压可以用其它的电流、电压来表示。换句话说，我们可以找一个量作为新的控制量，利用基尔霍夫定律、欧姆定律进行控制量的“转移”即变换，从而使原控制量所在支路也能与其它支路一样参与电路的等效变换。

在对电路进行等效化简时，原控制量与其所在支路消失了，但该支路的两个端纽却可以保留下来，因为它们实际上也是原始电路的两个节点，故它们也同时属于该支路相连接的外电路。而在变换后的电路中，这两个端纽之间的电压又可以用新的形式来表示，并参与电路的计算。在变换控制量的同时，受控源仍然可以当作独立电源来处理，即将受控电压源、电阻串联组合与受控电流源、电导的并联组合相互进行等效变换。这样，就有可能将含受控源的电路最终化简成单回路电路从而使计算过程变得简便。

由以上分析可知：用等效变换方法分析含受控源的电路时，控制量也是可以变换的，从而使原控制量所在支路与其它支路一样参与电路变换，也使等效变换这一方法更充分地发挥其化简电路的作用，使等效电路更为简单，运算更为简便；以原控制量所在支路的支路电压作为新控制量，简单、方便、容易掌握和运用。1

负反馈放大电路变换分析法的讨论对负反馈放大电路，可以认为信号只通过基本放大电路，从输入端传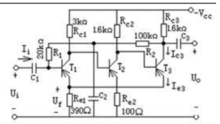送到输出端，反馈信号只通过反馈网络反馈到输入端，反馈系数与信号源内阻及负载无关。因此可以按照一定的变换规律得到即断开反馈又考虑了反馈网络负载效应的放大电路。由于可以直接从这个电路中求出反馈系数，故将其称为基本反馈电路。然后求出基本反馈电路的开环增益和反馈系数，再根据负反馈的一般公式，计算有反馈时的闭环增益、输入电阻和输出电阻，这种负反馈放大电路的分析方法既称为变换分析法。用变换分析法分析负反馈放大电路时，关键在于要按照一定的变换规律把负反馈放大电路变换为基本反馈电路，而反馈网络应包含在基本反馈电路中，但仅起到负载的作用。

负反馈放大电路变换为反馈电路的一般规律（1）如何从负反馈放大电路中找出基本反馈电路输出回路

从负反馈放大电路输入端看：如果是串联反馈 ,将负反馈放大电路输入端开路；如果是并联反馈，将负反馈放大电路输入端短路(Ui=0)；从负反馈放大电路输出端得到的交流通路即为基本反馈电路输出回路的交流通路。

（2）如何从负反馈放大电路中找出基本反馈电路输入回路

从负反馈放大电路输出端看：如果是电压反馈，将负反馈放大电路输出端短路(U0=0)；如果是并联反馈，将负反馈放大电路输出端开路(I0= 0)；从负反馈放大电路输入端得到的交流通路即为基本反馈电路输入回路的交流通路。经过以上变换，可求得即断开反馈又考虑了反馈网络负载效应的基本反馈电路。

负反馈放大电路动态参数的计算步骤(1) 确定反馈类型，依照变换分析法，从负反馈放大电路中求出基本反馈电路；

(2) 在基本反馈电路中求出反馈系数F，开环增益A；

(3) 求出反馈深度；

(4) 利用反馈深度，结合负反馈放大电路，求出闭环增益、输入电阻、输出电阻。

研究结论从以上分析举例可看出，对多级反馈放大电路，利用这种方法可归结为计算基本反馈电路的反馈系数和开环增益，然后利用负反馈的一般公式，结合负反馈放大电路，计算出有反馈时的闭环增益、输入电阻和输出电阻，优点是物理概念清楚，比较直观。2

本词条内容贡献者为:

张磊 - 副教授 - 西南大学