微分在数学中的定义:由函数B=f(A),得到A、B两个数集,在A中当dx靠近自己时,函数在dx处的极限叫作函数在dx处的微分,微分的中心思想是无穷分割。微分是函数改变量的线性主要部分。微积分的基本概念之一。12
发展历史萌芽时期
早在希腊时期,人类已经开始讨论「无穷」、「极限」以及「无穷分割」等概念。这些都是微积分的中心思想;虽然这些讨论从现代的观点看有很多漏洞,有时现代人甚至觉得这些讨论的论证和结论都很荒谬,但无可否认,这些讨论是人类发展微积分的第一步3。
例如公元前五世纪,希腊的德谟克利特(Democritus)提出原子论:他认为宇宙万物是由极细的原子构成。在中国,《庄子.天下篇》中所言的「一尺之捶,日取其半,万世不竭」,亦指零是无穷小量。这些都是最早期人类对无穷、极限等概念的原始的描述。
其他关于无穷、极限的论述,还包括芝诺(Zeno)几个著名的悖论:其中一个悖论说一个人永远都追不上一只乌龟,因为当那人追到乌龟的出发点时,乌龟已经向前爬行了一小段路,当他再追完这一小段,乌龟又已经再向前爬行了一小段路。芝诺说这样一追一赶的永远重覆下去,任何人都总追不上一只最慢的乌龟--当然,从现代的观点看,芝诺说的实在荒谬不过;他混淆了「无限」和「无限可分」的概念。人追乌龟经过的那段路纵然无限可分,其长度却是有限的;所以人仍然可以以有限的时间,走完这一段路。然而这些荒谬的论述,开启了人类对无穷、极限等概念的探讨,对后世发展微积分有深远的历史意味。
另外值得一提的是,希腊时代的阿基米德(Archimedes)已经懂得用无穷分割的方法正确地计算一些面积,这跟现代积分的观念已经很相似。由此可见,在历史上,积分观念的形成比微分还要早--这跟课程上往往先讨论微分再讨论积分刚刚相反。
十七世纪的大发展牛顿和莱布尼茨的贡献
中世纪时期,欧洲科学发展停滞不前,人类对无穷、极限和积分等观念的想法都没有什么突破。中世纪以后,欧洲数学和科学急速发展,微积分的观念也於此时趋於成熟。在积分方面,一六一五年,开普勒(Kepler)把酒桶看作一个由无数圆薄片积累而成的物件,从而求出其体积。而伽利略(Galileo)的学生卡瓦列里(Cavalieri)即认为一条线由无穷多个点构成;一个面由无穷多条线构成;一个立体由无穷多个面构成。这些想法都是积分法的前驱。
在微分方面,十七世纪人类也有很大的突破。费马(Fermat)在一封给罗贝瓦(Roberval)的信中,提及计算函数的极大值和极小值的步骤,而这实际上已相当於现代微分学中所用,设函数导数为零,然后求出函数极点的方法。另外,巴罗(Barrow)亦已经懂得透过「微分三角形」(相当於以dx、dy、ds为边的三角形)求出切线的方程,这和现今微分学中用导数求切线的方法是一样的。由此可见,人类在十七世纪已经掌握了微分的要领。
然而,直至十七世纪中叶,人类仍然认为微分和积分是两个独立的观念。就在这个时候,牛顿和莱布尼茨将微分及积分两个貌似不相关的问题,透过「微积分基本定理」或「牛顿-莱布尼茨公式」联系起来,说明求积分基本上是求微分之逆,求微分也是求积分之逆。这是微积分理论中的基石,是微积分发展一个重要的里程碑。
一元型
定义设函数y = f(x)在x的邻域内有定义,x及x + Δx在此区间内。如果函数的增量Δy = f(x + Δx) - f(x)可表示为 Δy = AΔx + o(Δx)(其中A是不依赖于Δx的常数),而o(Δx)是比Δx高阶的无穷小(注:o读作奥密克戎,希腊字母)那么称函数f(x)在点x是可微的,且AΔx称作函数在点x相应于自变量增量Δx的微分,记作dy,即dy = AΔx。函数的微分是函数增量的主要部分,且是Δx的线性函数,故说函数的微分是函数增量的线性主部(△x→0)。
通常把自变量x的增量 Δx称为自变量的微分,记作dx,即dx = Δx。于是函数y = f(x)的微分又可记作dy = f'(x)dx。函数的微分与自变量的微分之商等于该函数的导数。因此,导数也叫做微商。
当自变量X改变为X+△X时,相应地函数值由f(X)改变为f(X+△X),如果存在一个与△X无关的常数A,使f(X+△X)-f(X)和A·△X之差是△X→0关于△X的高阶无穷小量,则称A·△X是f(X)在X的微分,记为dy,并称f(X)在X可微。一元微积分中,可微可导等价。记A·△X=dy,则dy=f′(X)dX。例如:d(sinX)=cosXdX。
微分概念是在解决直与曲的矛盾中产生的,在微小局部可以用直线去近似替代曲线,它的直接应用就是函数的线性化。微分具有双重意义:它表示一个微小的量,因此就可以把线性函数的数值计算结果作为本来函数的数值近似值,这就是运用微分方法进行近似计算的基本思想。
推导设函数y = f(x)在某区间内有定义,x0及x0+△x在这区间内,若函数的增量Δy = f(x0 + Δx) − f(x0)可表示为Δy = AΔx + o(Δx),其中A是不依赖于△x的常数, o(Δx)是△x的高阶无穷小,则称函数y = f(x)在点x0是可微的。 AΔx叫做函数在点x0相应于自变量增量△x的微分,记作dy,即:dy=AΔx。微分dy是自变量改变量△x的线性函数,dy与△y的差是关于△x的高阶无穷小量,我们把dy称作△y的线性主部。得出: 当△x→0时,△y≈dy。 导数的记号为:(dy)/(dx)=f′(X),我们可以发现,它不仅表示导数的记号,而且还可以表示两个微分的比值(把△x看成dx,即:定义自变量的增量等于自变量的微分),还可表示为dy=f′(X)dX。4
几何意义设Δx是曲线y = f(x)上的点M的在横坐标上的增量,Δy是曲线在点M对 应Δx在纵坐标上的增量,dy是曲 线在点M的切线对应Δx在纵坐标上的增量。当|Δx|很小时,|Δy-dy|比|Δx|要小得多(高阶无穷小),因此在点M附近,我们可以用切线段来近似代替曲线段。4
应Δx在纵坐标上的增量,dy是曲 线在点M的切线对应Δx在纵坐标上的增量。当|Δx|很小时,|Δy-dy|比|Δx|要小得多(高阶无穷小),因此在点M附近,我们可以用切线段来近似代替曲线段。4
多元型当自变量为多个时,可得出多元微分的定义。一元微分一名常微分。
高阶型当自变量是多元变量时,导数的概念已经不适用了(尽管可以定义对某个分量的偏导数),但仍然有微分的概念。
定义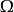
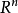 设f是从欧几里得空间(或者任意一个内积空间)中的一个开集射到
设f是从欧几里得空间(或者任意一个内积空间)中的一个开集射到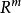 的一个函数。对于
的一个函数。对于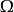 中的一点x及其在
中的一点x及其在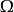 中的邻域
中的邻域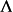 中的点x+h。如果存在线性映射A使得对任意这样的x+h,
中的点x+h。如果存在线性映射A使得对任意这样的x+h,

那么称函数f在点x处可微。线性映射A叫做f在点x处的微分,记作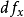 。
。
如果f在点x处可微,那么它在该点处一定连续,而且在该点的微分只有一个。为了和偏导数区别,多元函数的微分也叫做全微分或全导数2。
当函数在某个区域的每一点x都有微分 时,可以考虑将x映射到
时,可以考虑将x映射到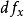 的函数:
的函数:

这个函数一般称为微分函数。
性质如果f是线性映射,那么它在任意一点的微分都等于自身。
在Rn(或定义了一组标准基的内积空间)里,函数的全微分和偏导数间的关系可以通过雅可比矩阵刻画:
设f是从Rn射到Rm的函数,f=(f1,f2,...fm),那么:
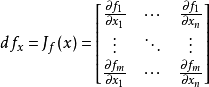
具体来说,对于一个改变量: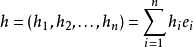 ,微分值:
,微分值:
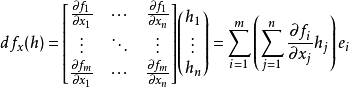
可微的必要条件:如果函数f在一点x_0处可微,那么雅克比矩阵的每一个元素 都存在,但反之不真。
都存在,但反之不真。
可微的充分条件:如果函数f在一点x_0的雅克比矩阵的每一个元素\frac{\partial f_i}{\partial x_j}(x_0)都在x_0连续,那么函数在这点处可微,但反之不真。5
例子函数  是一个从R2射到R3的函数。它在某一点(x, y)的雅可比矩阵为:
是一个从R2射到R3的函数。它在某一点(x, y)的雅可比矩阵为:
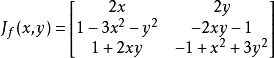
微分为: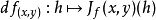 ,也就是:
,也就是:

我们对函数y进行微分,得出导数 ,由于微分只进行了一次,所以
,由于微分只进行了一次,所以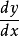 又被称为一阶导数。
又被称为一阶导数。
这时,我们微分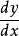 ,得出
,得出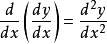 ,那么
,那么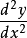 被称为二阶导数。
被称为二阶导数。
同理,我们可以得到三次导数及更高次的导数, (n
(n 2)被称为n阶导数。2
2)被称为n阶导数。2
切线微分当自变量为固定值
需要求出曲线上一点的斜率时,前人往往采用作图法,将该点的切线画出,以切线的斜率作为该点的斜率。然而,画出来的切线是有误差的,也就是说,以作图法得到的斜率并不是完全准确的斜率2。微分最早就是为了从数学上解决这一问题而产生的。
以y=x2 为例,我们需要求出该曲线在(3,9)上的斜率,当△x与△y的值越接近于0,过这两点直线的斜率就越接近所求的斜率m,当△x与△y的值变得无限接近于0时,直线的斜率就是点的斜率。
当x = 3 +Δx 时,y = 9+ Δy,也就是说,
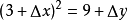
 (展开)
(展开)
 (两边减去9)
(两边减去9)

(两边除以△x)
∵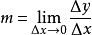 (m为曲线在(3,9)上的斜率,
(m为曲线在(3,9)上的斜率,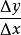 为直线斜率)
为直线斜率)
∴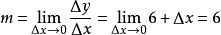
我们得出, 在点(3,9)处的斜率为6。
在点(3,9)处的斜率为6。
当自变量为任意值
在很多情况下,我们需要求出曲线上许多点的斜率,如果每一个点都按上面的方法求斜率,将会消耗大量时间,计算也容易出现误差,这里我们仍以 为例,计算图象上任意一点的斜率m。
为例,计算图象上任意一点的斜率m。
假设该点为(x,y),做对照的另一点为(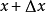 ,
,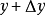 ),我们按上面的方法再计算一遍:
),我们按上面的方法再计算一遍:
 (展开)
(展开)
 (
( ,两边减去y)
,两边减去y)
 (两边除以△x)
(两边除以△x)
∵
∴
我们得出,y=x2 在点(x,y)处的斜率为2x。
从二次函数到幂函数
通过以上的方法,我们可以得出x的二次函数在任意一点上的斜率,但是这远远不够。我们需要把这种方法扩充到所有的幂函数。假设有函数 ,假设函数上有一点(x,y)和另一点(x+Δx,y+Δy) ,我们可以这样计算斜率:
,假设函数上有一点(x,y)和另一点(x+Δx,y+Δy) ,我们可以这样计算斜率:
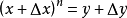
 (二项展开式)
(二项展开式)
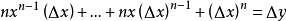 (
( )
)
 (两边除以△x)
(两边除以△x)
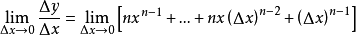 (加上极限)
(加上极限)
 (其他项均带有△x,在△x→0的情况下都可以视为等于0)
(其他项均带有△x,在△x→0的情况下都可以视为等于0)
我们得出,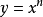 在点(x,y)处的斜率为
在点(x,y)处的斜率为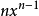 。6
。6
从幂函数到单项式
我们可以把幂函数的斜率扩展到单项式函数 的斜率,依然假设有两点(x,y)和
的斜率,依然假设有两点(x,y)和 :
:
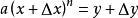
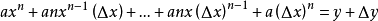 (二项展开式)
(二项展开式)
 (
( ,两边减去y)
,两边减去y)
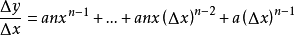 (两边除以△x)
(两边除以△x)
 (加上极限)
(加上极限)
 (其他项均带有△x,在△x→0的情况下都可以视为等于0)
(其他项均带有△x,在△x→0的情况下都可以视为等于0)
我们得出,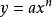 在点(x,y)处的斜率为
在点(x,y)处的斜率为 。
。
这就是微分的基本公式,“基本法则”目录有详细的说明。
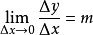 被记作dy/dx=m 。
被记作dy/dx=m 。
单项式
当函数为单项式 (a和n为常数)的形式时,有基本公式:
(a和n为常数)的形式时,有基本公式:
注意:基本公式极为重要,在学习更为复杂的运算法则前请务必牢记。
多项式
当函数为几个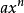 形式的单项式的和或差时,这个函数的导数只需在原函数的导数上进行加减即可。
形式的单项式的和或差时,这个函数的导数只需在原函数的导数上进行加减即可。
以函数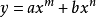 为例,将其拆分为两个函数
为例,将其拆分为两个函数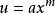 和
和 ,且
,且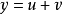 。
。
可以得出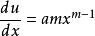 ,
,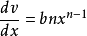 。
。
y=u+v
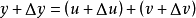

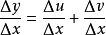


同理可以得出
最后得出公式:

有了这两个公式,我们可以对大部分常见的初等函数求导。
注意:**f'(x)**是函数f(x)的导数。6
运算法则基本法则
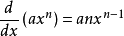

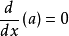
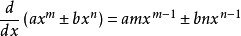
连锁律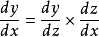 (微分连锁律)
(微分连锁律)

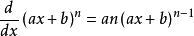

乘法律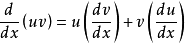 (微分乘法律)
(微分乘法律)


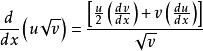
除法律 (微分除法律)
(微分除法律)

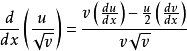
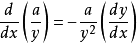
导数导数一正弦函数****的导数
假设正弦函数y=sin x(x的单位为弧度)上有一点(x,y)和另一点(x+δx,y+δy):
d/dx(sin x)
=limδx→0 δy/δx
=limδx→0 [sin (x+δx)-sin x]/δx
=limδx→0 2[cos 0.5(2x+δx)][sin 0.5(δx)]/δx (sin A-sin B=2[cos 0.5(A+B)][sin 0.5(A-B)])
=limδx→0 [cos 0.5(2x+δx)][sin 0.5(δx)]/0.5δx (两边除以2)
=limδx→0 [cos 0.5(2x+δx)]×[sin 0.5(δx)]/0.5δx
=limδx→0 [cos 0.5(2x+δx)]×limδx→0 [sin 0.5(δx)]/0.5δx
=cos 0.5(2x)×1 (limθ→0 (sin θ)/θ=1)
=cos x
最后得出d/dx(sin x)=cos x。
余弦函数****的导数
我们知道cos x=sin(π/2-x),所以d/dx(cos x)=d/dx[sin (π/2-x)]。
假设π/2-x=u,我们可以用连锁律对余弦函数y=cos x求导:
d/dx(cos x)
=d/dx[sin (π/2-x)]
=d/du[sin (π/2-x)]×d/dx(π/2-x) (连锁律)
=cos (π/2-x)×(-1) (d/dx(sin x)=cos x)
=-cos (π/2-x)
=-sin x (cos (π/2-x)=sin x)
最后得出d/dx(cos x)=-sin x。
正切函数****的导数
由于正切函数tan x=(sin x)/(cos x),我们可以用除法律对其求导:
d/dx(tan x)
=d/dx[(sin x)/(cos x)] (tan x=(sin x)/(cos x))
=[(cos x)d/dx(sin x)-(sin x)d/dx(cos x)]/(cos^2 x) (除法律)
=[cos^2 x-(sin x)(-sin x)]/cos^2 x
=(cos^2 x+sin^2 x)/cos^2 x
=1/cos^2 x
=sec^2 x
最后得出d/dx(tan x)=sec^2 x。
三角函数****的应用1
当我们遇到y=sin/cos/tan u(u是自变量为x的函数且常为ax+b的形式)这类函数的时候,可以使用连锁律求导:
①y=sin u
d/dx(sin u)
=(dy/du)(du/dx) (连锁律)
=(cos u)(du/dx)
当u的形式为ax+b时,du/dx=a,所以:
d/dx[sin(ax+b)]=a[cos(ax+b)]
②y=cos
当u的形式为ax+b时,du/dx=a,所以:
d/dx[cos(ax+b)]=-a[sin(ax+b)]
③y=tan u
d/dx(tan u)
=(dy/du)(du/dx) (连锁律)
=(sec^2 u)(du/dx)
当u的形式为ax+b时,du/dx=a,所以:
d/dx[tan(ax+b)]=a[sec^2(ac+b)]
三角函数的应用2
有时我们需要对y=sin^n x或y=cos^n x(n为常数)这类函数求导,使用连锁律也可以解决:
这里我们使用“连锁律的应用1”中得到的公式:d/dx(y^n)=[ny^(n-1)](dy/dx)
①y=sin^n x
dy/dx
=n[sin^(n-1) x]d/dx(sin x)
=n[sin^(n-1) x](cos x)
②y=cos^n x
dy/dx
=n[cos^(n-1) x]d/dx(cos x)
=-n[cos^(n-1) x](sin x)
得出公式:
d/dx(sin^n x)=n[sin^(n-1) x](cos x)
d/dx(cos^n x)=-n[cos^(n-1) x](sin x)
导数二自然指数函数的导数
在画图软件里,我们可以看出在函数y=e^x上任意一点(x,y)的斜率均等于y。也就是说,m=dy/dx=y。
因此,函数e^x的导数由以下公式获得
证明:y=e^x,
y+dy=e^(x+dx),
dy=e^(x+dx)-e^x
=e^x(e^dx-1)
=e^x(1+dx+dx^2/2!+……+dx^n/n!-1){e^a=1+a+a^n/n!(n∈N)}
≈dxe^x
∴d/dx(e^x)=e^x
自然指数函数的应用
我们可以使用连锁律对y=e^u(u是自变量为x的函数)求导:
dy/dx
=(dy/du)(du/dx) (连锁律)
=[d/du(e^u)](du/dx)
=(e^u)(du/dx)
最后得出:
d/dx(e^u)=(e^u)(du/dx)
如果u的形式为ax+b(a和b均为常数),那么du/dx=a,可以得出:
d/dx[e^(ax+b)]=ae^(ax+b)
自然对数****函数的导数
我们可以通过d/dx(e^x)=e^x对自然对数函数y=ln x求导:
y=ln x
x=e^y
d/dx(x)=d/dx(e^y)
d/dx(x)=d/dy(e^y)(dy/dx) (连锁律)
d/dx(x)=(e^y)(dy/dx)
(e^y)(dy/dx)=1
x(dy/dx)=1 (x=e^y)
dy/dx=1/x
最后得出:
d/dx(ln x)=1/x
自然对数****函数的应用
我们可以使用连锁律对y=ln u(u是自变量为x的函数)求导:
dy/dx
=(dy/du)(du/dx) (连锁律)
=[d/du(ln u)](du/dx)
=(1/u)(du/dx)
可以得出:
d/dx(ln u)=(1/u)(du/dx)
如果u的形式为ax+b(a和b均为常数),那么du/dx=a,可以得出:
d/dx[ln (ax+b)]=a/(ax+b)
特殊导数三角函数
d/dx(sin x)=cos x
d/dx(cos x)=-sin x
d/dx(tan x)=sec^2 x
d/dx[sin(ax+b)]=a[cos(ax+b)]
d/dx[cos(ax+b)]=-a[sin(ax+b)]
d/dx[tan(ax+b)]=a[sec^2(ax+b)]
d/dx(sin^n x)=n[sin^(n-1) x](cos x)
d/dx(cos^n x)=-n[cos^(n-1) x](sin x)
自然指数函数
d/dx(e^x)=e^x
d/dx(e^u)=(e^u)(du/dx)
d/dx[e^(ax+b)]=ae^(ax+b)
自然对数函数
d/dx(ln x)=1/x
d/dx(ln u)=(1/u)(du/dx)
d/dx[ln (ax+b)]=a/(ax+b)
微分应用法线
我们知道,曲线上一点的法线和那一点的切线互相垂直,微分可以求出切线的斜率,自然也可以求出法线的斜率。
假设函数y=f(x)的图象为曲线,且曲线上有一点(x1,y1),那么根据切线斜率的求法,就可以得出该点切线的斜率m:
m=dy/dx在(x1,y1)的值
所以该切线的方程式为:
y-y1=m(x-x1)
由于法线与切线互相垂直,法线的斜率为-1/m且它的方程式为:
y-y1=(-1/m)(x-x1)
增函数与减函数
微分是一个鉴别函数(在指定定义域内)为增函数或减函数的有效方法。
鉴别方法:dy/dx与0进行比较,dy/dx大于0时,说明dx增加为正值时,dy增加为正值,所以函数为增函数;dy/dx小于0时,说明dx增加为正值时,dy增加为负值,所以函数为减函数。
例1:分析函数y=x^2-1 的增减性
∵y=x^2-1
∴dy/dx=2x
当x>0时,dy/dx>0,所以函数y=x^2-1在x>0时是增函数;
当x




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国