[科普中国]-样本容量

样本容量是指一个样本中所包含的单位数，一般用n 表示，它是抽样推断中非常重要的概念。样本容量的大小与推断估计的准确性有着直接的联系，即在总体既定的情况下，样本容量越大其统计估计量的代表性误差就越小，反之,样本容量越小其估计误差也就越大。1

简介又称“样本大小”，在一个样本中所包含的个案或单元数。一般来说，样本容量主要由精确度、同质性、财力、抽样类型、分析类别等因素决定。在抽样调查中，样本容量的确定很重要。因为样本容量太大，会造成人力、物力和财力的很大浪费；样本容量太小，会使抽样误差太大，使调查结果与实际情况相差很大,影响调查的效果。2

解释样本容量的大小涉及到调研中所要包括的单元数。样本容量是对于你研究的总体而言的，是在抽样调查中总体的一些抽样。比如：中国人的身高值为一个总体，你随机取一百个人的身高，这一百个人的身高数据就是总体的一个样本。某一个样本中的个体的数量就是样本容量。**注意：不能说样本的数量就是样本容量，因为总体中的若干个个体只组成一个样本。**样本容量不需要带单位。

在假设检验里样本容量越大越好。但实际上不可能无穷大，就像你研究中国人的身高不可能把所有中国人的身高都量一量一样。2

详细内容相关定义回归分析是从已经发生的经济活动的样本数据中寻找经济活动中内含的规律性，它对样本数据具有很强的依赖性。样本的容量太小会导致参数估计值的大小和符号违反经济理论和实际经验。从建模需要来讲，样本容量越大越好，但收集与整理样本数据是一件困难的工作，因此，选择合适的样本容量，既能满足模型估计的需要，又能减轻收集数据的困难，是一个重要的实际问题。

(1) 最小样本容量

所谓“最小样本容量”，即从普通最小二乘法原理出发，欲得到参数估计量，不管其质量如何，所要求的样本容量的下限，它是：n≥k+1

其中，k为解释变量的数目。

(2) 满足基本要求的样本容量

一般经验认为，当n≥30或者至少n≥3(k+1)时，才能满足模型估计的基本要求。3

最优选择在确定抽样方法和样本量的时候，既要考虑调查的目的、调查性质和精度要求（抽样误差）等，又要考虑实际操作的可实施性，非抽样误差的控制、经费预算等。专业调查公司在这方面会根据您的情况及调查性质，进行综合权衡，达到一个最优的样本容量的选择。

意义合理确定样本容量的意义：

1.样本容量过大，会增加调查工作量，造成人力、物力、财力、时间的浪费；

2.样本容量过小，则样本对总体缺乏足够的代表性，从而难以保证推算结果的精确度和可靠性；

3.样本容量确定的科学合理，一方面，可以在既定的调查费用下，使抽样误差尽可能小，以保证推算的精确度和可靠性；另一方面，可以在既定的精确度和可靠性下，使调查费用尽可能少，保证抽样推断的最大效果。

样本个数所谓样本个数，就是样本可能的数目，指的是从一个总体中可能抽取的样本数。例如一个容量为500的总体，从中抽取100个不同的子集做抽样调查，则样本个数为100。

公式和方法公式具体确定样本量还有相应的统计学公式，不同的抽样方法对应不同的公式。根据样本量计算公式，我们知道，样本量的大小不取决于总体的多少，而取决于(1) 研究对象的变化程度；(2) 所要求或允许的误差大小（即精度要求）；(3) 要求推断的置信程度。也就是说，当所研究的现象越复杂，差异越大时，样本量要求越大；当要求的精度越高，可推断性要求越高时，样本量越大。因此，如果不同城市分别进行推断时，大城市多抽，小城市少抽这种说法原则上是不对的。在大城市抽样太大是浪费，在小城市抽样太少没有推断价值。

计算方法确定样本容量的大小是比较复杂的问题，既要有定性的考虑也要有定量的考虑。从定性的方面考虑样本量的大小，其考虑因素有：决策的重要性，调研的性质，变量个数，数据分析的性质，同类研究中所用的样本量，发生率，完成率，资源限制等。具体地说，更重要的决策，需要更多的信息和更准确的信息，这就需要较大的样本；探索性研究，样本量一般较小，而结论性研究如描述性的调查，就需要较大的样本；收集有关许多变量的数据，样本量就要大一些，以减少抽样误差的累积效应；如果需要采用多元统计方法对数据进行复杂的高级分析，样本量就应当较大；如果需要特别详细的分析，如做许多分类等，也需要大样本。针对子样本分析比只限于对总样本分析，所需样本量要大得多。

公式：

（1）重复抽样方式下：

变量总体重复抽样计算公式：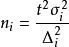

属性总体重复抽样：

（2）不重复抽样方式下：

变量总体不重复抽样计算公式：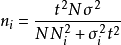

属性总体不重复抽样：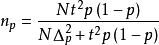

相关资料在一些生产过程中，过程均值的正向飘移与负向飘移对生产者意味着不同损失。提出了两种非对称样本容量均值图，利用马氏链方法研究了控制图的控制性质。计算结果显示，对于小于1.5个过程标准差的过程均值飘移，非对称样本容量均值图在兼顾一方向飘移的同时能更加快速地发现另一方向飘移，而警戒限的加入加快了控制图发现过程均值一个方向漂移的速度。4

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学