罗尔(Rolle)中值定理是微分学中一条重要的定理,是三大微分中值定理之一,其他两个分别为:拉格朗日(Lagrange)中值定理、柯西(Cauchy)中值定理。
罗尔定理描述如下:
如果 R 上的函数 f(x) 满足以下条件:(1)在闭区间 [a,b] 上连续,(2)在开区间 (a,b) 内可导,(3)f(a)=f(b),则至少存在一个 ξ∈(a,b),使得 f'(ξ)=0。
证明过程证明:因为函数 f(x) 在闭区间[a,b] 上连续,所以存在最大值与最小值,分别用 M 和 m 表示,分两种情况讨论:
1. 若 M=m,则函数 f(x) 在闭区间 [a,b] 上必为常函数,结论显然成立。
2. 若 M>m,则因为 f(a)=f(b) 使得最大值 M 与最小值 m 至少有一个在 (a,b) 内某点ξ处取得,从而ξ是f(x)的极值点,又条件 f(x) 在开区间 (a,b) 内可导得,f(x) 在 ξ 处取得极值,由费马引理推知:f'(ξ)=0。
另证:若 M>m ,不妨设f(ξ)=M,ξ∈(a,b),由可导条件知,f'(ξ+)=0,又由极限存在定理知左右极限均为 0,得证。1
几何意义若连续曲线y=f(x) 在区间 [a,b] 上所对应的弧段 AB,除端点外处处具有不垂直于 x 轴的切线,且在弧的两个端点 A,B 处的纵坐标相等,则在弧 AB 上至少有一点 C,使曲线在C点处的切线平行于 x 轴。1
几种特殊情况**(1)有界开区间上的有界函数**
若函数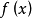 在区间
在区间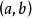 上连续且可导,并有
上连续且可导,并有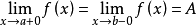 ,则至少存在一个
,则至少存在一个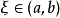 ,使得
,使得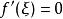 。
。
(2)有界区间上的无界函数
若函数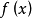 在区间
在区间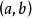 上连续且可导,并有
上连续且可导,并有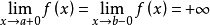 (或
(或 ),则至少存在一个
),则至少存在一个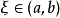 ,使得
,使得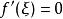 。
。
(3)无界区间上的有界函数
若函数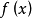 在区间
在区间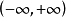 上连续且可导,并有
上连续且可导,并有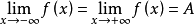 ,则至少存在一个
,则至少存在一个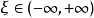 ,使得
,使得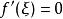 。
。
(4)无界区间上的无界函数
若函数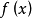 在区间
在区间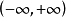 上连续且可导,并有
上连续且可导,并有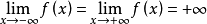 (或
(或 ),则至少存在一个
),则至少存在一个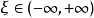 ,使得
,使得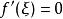 。
。
(5)半无界区间上的有界函数
若函数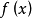 在区间[
在区间[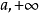 )上连续且可导,并有
)上连续且可导,并有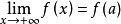 ,则至少存在一个
,则至少存在一个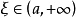 ,使得
,使得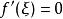 。
。
(6)半无界区间上的无界函数
若函数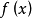 在区间[
在区间[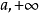 )上连续且可导,并有
)上连续且可导,并有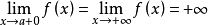 (或
(或 ),则至少存在一个
),则至少存在一个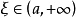 ,使得
,使得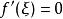 。
。
证明
这里仅选择特殊情况(2)、(3)加以证明,其余证明的思路大致类似。
定理 若函数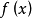 在区间
在区间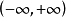 上连续且可导,并有
上连续且可导,并有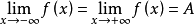 。则至少存在一个
。则至少存在一个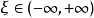 ,使得
,使得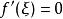 。1
。1
**证明:**至少可取到一点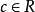 ,使
,使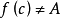 ,否则
,否则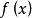 恒等于
恒等于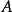 ,对于任意的实数
,对于任意的实数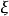 ,都有
,都有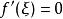 。
。
不妨设 ,取
,取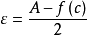 ,显然
,显然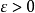 。根据极限定义,由
。根据极限定义,由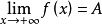 可得
可得
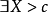 ,当
,当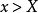 时,有
时,有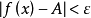 ,
,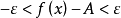 ,
,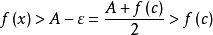 ,
,
任取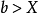 ,则有
,则有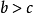 ,
,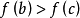 。
。
利用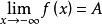 ,类似地可知存在
,类似地可知存在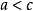 ,使
,使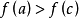 。
。
于是,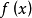 在闭区间
在闭区间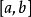 上连续,则在闭区间
上连续,则在闭区间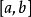 上必有
上必有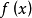 的最小值点
的最小值点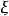 ,由于闭区间
,由于闭区间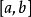 的两个端点都不可能是
的两个端点都不可能是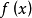 的最小值点,由此可知
的最小值点,由此可知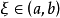 ,根据费马定理可知
,根据费马定理可知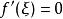 。
。
定理 若函数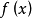 在区间
在区间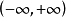 上连续且可导,并有
上连续且可导,并有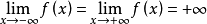 。则至少存在一个
。则至少存在一个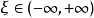 ,使得
,使得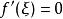 。1
。1
证明: 任取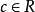 ,因为
,因为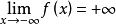 ,所以至少存在一点
,所以至少存在一点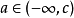 ,使
,使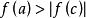 。
。
类似地由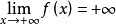 可知存在一点
可知存在一点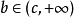 ,使
,使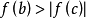 。
。
这就有了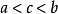 且
且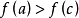 ,
,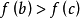
于是,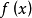 在闭区间
在闭区间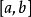 上连续,则在闭区间
上连续,则在闭区间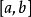 上必有
上必有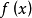 的最小值点
的最小值点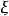 ,由于闭区间
,由于闭区间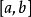 的两个端点都不可能是
的两个端点都不可能是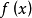 的最小值点,由此可知
的最小值点,由此可知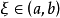 ,根据费马定理可知
,根据费马定理可知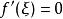 。
。
范例解析用罗尔中值定理证明:方程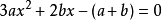 在 (0,1) 内有实根。
在 (0,1) 内有实根。
证明: 设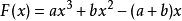
则 F(x) 在 [0,1] 上连续,在 (0,1) 内可导,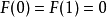 ,所以由罗尔中值定理,至少存在一点
,所以由罗尔中值定理,至少存在一点 ,使得
,使得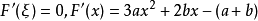 ,所以
,所以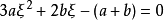 ,所以ξ是方程
,所以ξ是方程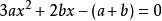 在 (0,1) 内的一个实根。
在 (0,1) 内的一个实根。
结论得证。2
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国