[科普中国]-相互独立事件

在概率论里，说两个事件是独立的，直觉上是指一次实验中一事件的发生不会影响到另一事件发生的概率。例如，骰子掷出“6”的事件和骰子掷出“1”的事件是相互独立的。类似地，两个随机变量是独立的，若其在一事件给定观测量的条件概率分布和另一事件没有被观测的概率分布是一样的。相互独立事件（independent events)就是事件A（或B）是否发生对事件B（A）发生的概率没有影响，这样的两个事件叫做相互独立事件。1

定义A和B中至少有一件事情发生：A∪B；A与B同时发生：A∩B，AB；如果P(A B) =P(A) P(B)，称A,B 相互独立。1

标准的定义为：两个事件A和B是独立的当且仅当Pr(A∩B) = Pr(A)Pr(B)。这里，A∩B是A和B的交集，即为A和B两个事件都会发生的事件。更一般地，任意个事件都是互相独立的当且仅当对其任一有限子集A1, ...,An，会有

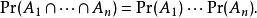这被称为独立事件的乘法规则。

若两个事件A和B是独立的，则其B给之A的条件概率和A的“无条件概率”一样，即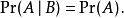至少有两个理由可以解释为何此一叙述不可以当做独立性的定义：(1)A和B两个事件在此叙述中并不对称，及(2)当概率为0亦可包含于此叙述时，会有问题产生。若回想条件概率Pr(A|B)的定义为 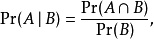(只要Pr(B) ≠ 0 )，则上面的叙述则会等价于

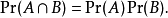即为上面所给定的标准定义。注意独立性并不和它在地方话里的有相同的意思。例如，一事件独立于其自身当且仅当

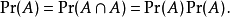亦即，其概率不是零就是一。因此，当一事件或其补集几乎确定会发生，它即是独立于其本身。例如，若事件A从单位区间的连续型均匀分布上选了0.5，则A是独立于其自身的，尽管重言式地，A完全决定了A。

性质（1）A,B独立等价于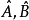 独立，其中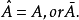

（2）A,B独立，则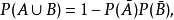 是A的对立事件。1

推导相互独立事件的公式由条件概率推得：

以任意两事件AB为例：

P(AB)=P(A)P(B|A)或P(AB)=P(B)P(A|B)。

P(B|A)表示A发生的条件下B发生的概率。所以，当AB相互独立时，P(B|A)=P(B)。

推广到n个任意事件A1,A2,A3……An：

P(A1A2A3……An)=P(A1)P(A2|A1)P(A3|A1A2)P(A4|A1A2A3)……P(An|A1A2A3……An-1)。

注：P(A4|A1A2A3)表示A1A2A3同时发生的条件下A4发生的概率。

如：A、B、C为事件，P(ABC)>0，则P(AB|C)=P(A|C)P(B|C)充要条件是P(B|AC)P(B|AC)。

与集合的关系相互独立事件其实没有明确的相交与互斥关系。因为相交就意味着事件相互影响，互斥意味着事件不可能同时发生；而相互独立事件既有可能同时发生，也有可能不同时发生，那么它们到底是什么关系呢？其实这就是概率问题，可能同时发生，也有可能不同时发生，这和物理中的波粒二象性有些类似，如果一定要画图像，它们的图像就是动态的。

相互独立事件之间没有相互的影响，故其中一个事件的发生不影响另一个事件的发生概率，则必然存在两个事件同时发生的可能性（除非有一个事件概率为0）。

实际上，相互独立事件是有相交关系的事件间关系的特例。相互独立事件间必然有P(A I B)= P(A)及P(B I A)= P(B)，关于这一点可以这么理解：P(A I B)是事件B发生后事件A发生的概率，通常的计算是P(AB)/P(B)，实际意义是事件A和事件B同时发生的可能性在事件B发生（包含事件A同时发生的情况）的可能性中占的比率（即在事件B的范围内事件A的发生概率），由于A和B相互独立，事件B的发生不对事件A的发生造成影响，即在事件B的范围内事件A的发生概率和整个样本空间中事件A发生的概率一样，所以有P(A I B)= P(A)和 P(B I A)= P(B)。

推广n个事件A1,A2,……,An。1

P(AiAj)=P(Ai)P(Aj),1≤i