[科普中国]-圆锥曲线论

圆锥曲线最早是由古希腊学者梅内克谬斯(Menaechmus)进行系统研究的，他用顶角分别为直角、锐角和钝角，三种直圆锥以不过顶点而垂直一条母线的平面截割这三种圆锥曲面，而分别得到抛物线、椭圆和双曲线的一支。

简介圆锥曲线亦称圆锥截线。简称锥线。一类重要的二次曲线。它是不过圆锥顶点的平面与圆锥面相交而成的曲线。

设圆锥的半顶角为α，平面与圆锥的轴所成的角为θ：

当θ=α 时，截面和圆锥的一条母线平行，交线是抛物线；

当 α0，c²=a²+b²。

参数方程：x=asecθ；y=btanθ （θ为参数）。

抛物线文字语言定义：平面内一个动点到一个定点与一条定直线的距离之比是等于1。定点是抛物线的焦点，定直线是抛物线的准线。

参数方程

x=2pt² ，

y=2pt (t为参数)，

t=1/tanθ（tanθ为曲线上点与坐标原点确定直线的斜率）特别地，t可等于0。

直角坐标

y=ax²+bx+c （开口方向为y轴，a≠0） x=ay²+by+c （开口方向为x轴，a≠0)。

离心率椭圆，双曲线，抛物线这些圆锥曲线有统一的定义：平面上，到定点的距离与到定直线的距离的比e是常数的点的轨迹叫做圆锥曲线。且当0PF2)；

|PF2|=a-ex(PF2b>0)

x²/a²-y²/b²=1 (a>0,b>0)

y²=2px (p>0)

中点弦问题已知圆锥曲线内一点为圆锥曲线的一弦中点，求该弦的方程：

1、联立方程法。

用点斜式设出该弦的方程（斜率不存在的情况需要另外考虑），与圆锥曲线方程联立求得关于x的一元二次方程和关于y的一元二次方程，由韦达定理得到两根之和的表达式，再由中点坐标公式和两根之和的具体数值，求出该弦的方程。

2、点差法（代点相减法）

设出弦的两端点坐标(x₁,y₁)和(x₂,y₂)，代入圆锥曲线的方程，将得到的两个方程相减，运用平方差公式得[(x₁+x₂)(x₁-x₂)]/a²+[(y₁+y₂)(y₁-y₂)/b²]=0

由斜率为(y₁-y₂)/(x₁-x₂），可以得到斜率的取值（使用时注意判别式的问题）

统一方程平面直角坐标系内的任意圆锥曲线可用如下方程表示：

其中，α∈[0,2π)，p>0，e≥0。

①e=1时，表示以F(g,h)为焦点，p为焦点到准线距离的抛物线。其中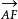与极轴夹角α（A为抛物线顶点）。

②0