[科普中国]-电子静止质量

电子静止质量是物理学的一个基本常数，正电子的静止质量等于电子的静止质量，其符号表示为me，数值大小为9.109 38215(45)×10-31 kg。

基本介绍电子〔静〕质量是电子静止状态时所具有的质量，符号为me。原子物理学和核物理学的量。SI单位：kg(千克)。并用的非SI单位：u(原子质量单位)。1 u=(1.660 540 2±0.000 001 0)×10-27 kg。me=9.109 389 7±0.000 005 4)×10-31 kg=(5. 485 799 03±0.000 000 13)×10-4u。

“电子静止质量”在不同场所都有出现。“电子静止质量”与电荷一起构建了最重要的基本粒子电子；“电子静止质量”与电荷共同约定了电子的有效尺寸——电子等效直径d；两个“电子静止质量”之间的万有引力与两个电荷之间的静电力，于相同力学条件下的力度比D，是最重要的物理常数之一；“电子静止质量”还可以整装地从正能态变成负能态，成为狄拉克海中的负能态电子的基本成分。以上陈述说明，“电子静止质量”是一个特殊意义的质量集团。我们暂且不去考虑它是不是最小的质量体，我们只在承认和利用“电子静止质量”的稳定的质量恒值状态，以及与这个质量恒值相关的几个有意义的力学常数：比如电子体积v，亦为“电子静止质量”的体积常数；比如质心相距为d时的两个“电子静止质量”间的万有引力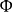 ，也是一个特殊意义的常数等。把“电子静止质量”想象为一种特定的质量单元，同静电的单元“电荷”相对仗，就是“质元”。

起源人们是从认识电子开始而知道原子核的，我们平常所用的电也来自于这种微小粒子的快速流动。科学家是怎么发现电子的呢?这一切又缘于阴极射线。

19世纪后，科学家们对电有了更多的认识，开始从事与气体放电现象有关的实验研究。1867年，德国科学家希托夫发现，如果将金属薄片放在真空放电管的阴极和产生荧光的管壁之间，有清晰的阴影产生，说明产生荧光的是一种起源于阴极、沿直线前进的射线，而且它能被磁铁偏转，说明带有电荷，人们称此为“阴极射线”。

这一现象引起英国科学家汤姆逊的浓厚兴趣。1897年，汤姆逊根据阴极射线在电场和磁场作用下的偏转，判定这是一种带电荷的粒子流，又用实验测定出这些粒子的电荷与其质量的比率为氢离子的千分之一。

后来，英国科学家克鲁克斯发明一种新的高真空度气体放电管，通上高压电后，阴极发射出强烈的荧光，照射在阴极对面的玻璃壁上，如果在阴极和玻璃壁之间放置一个小叶轮，轮叶就会开始转动，说明这种射线具有热效应和动量。

当时人们唯一知道的带电粒子是原子的负离子，但阴极射线粒子不可能是这种负离子，因为它受电磁场的偏转如此强。这只有两种可能，要么就是它的质量很小，要么就是它具有非常高的电荷。汤姆逊最终测定出阴极射线粒子的电荷同电解中氢离子所带的电荷是同一数量级，从而证明了阴极射线粒子的质量确实只是氢离子的千分之一。

汤姆逊还发现，无论是改变放电管中气体的成分，还是改变阴极材料，阴极射线的粒子都是相同的，而且不论是由于强电场的电离、紫外光的照射、正离子的轰击、金属受灼热还是放射性物质的自发辐射，都发射出相同的带电粒子，说明这些粒子一定是从金属原子中被撞击出来的，因此它必定是组成原子的一种更小的粒子。汤姆逊用令人信服的证据表明，原子并非像人们以往所认为的那样是物质最终不可分割的基本粒子。汤姆逊当时把它称作“微粒”，后来改称“电子”。

这种观念在当时令人震惊，但其后越来越多的实验发现证实了这一点。在1909年，美国物理学家密立根通过油滴实验，精确地测定出微小油滴上所带的电子电荷值，再次证明了电荷的不连续性和电子的存在。这些发现将人们进一步带人到原子世界的内部。汤姆逊因此获得1906年诺贝尔物理学奖，密立根获得1923年诺贝尔物理学奖。

根据实验测定结果，电子的质量为氢原子质量的1/1837，即9.10×10-28kg1。

相关概念质元定义“电子静止质量”为一个恒定的质量团粒，称为“质元”Unitmass，其质量用m代表，其占有空间表达为【】，其体积即是电子体积v，其实体表示为【m】。定义负值的“电子静止质量”亦是一个恒定的质量团粒，称作“负质元”Negunitmass，用m-代表它的负值质量，其占有空间同样表达为【】，其体积同为v，其实体表示为【m-】。为了引进无法回避的新概念术语，介绍了上述几个汉语和英语的新词汇。

质元体积就是电子体积，负质元体积又同质元体积一样，所以v为质元体积、负质元体积以及电子体积的共同表达，电子等效直径d同样为质元、负质元、电子三者的一维尺寸的共同表达，也可称之为“质元等效直径”。于是有

【】

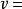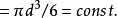
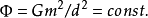
【】和 都是恒值。显然，“质元等效直径”d的意义就是质元体积【】的一维标识，而v则是质元体积【】的三维标识。 是质心相距为d时的任意两个质元之间的万有引力，它可以被看成万有引力作用的一个特定的单位。

电子的二元结构表达为【m e】。如果令符号【+】代表质元实体【m】，电子二元结构的表达形式【+e】，可以更加接近实际的物理图像——质元包容中心点电荷。

【+】=【m】

【+e】=【m e】

两个无扰状态的质元A与B之间给出的最强重力作用配位是，两个质元球体紧密相切。这时两球的质心距离最短，恰为d。如图3所示。这种配位下的两质元之间的万有引力大小，恰为一个常数单元

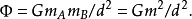
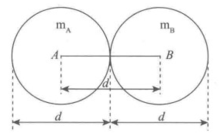
定义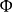 为“质量力量子”或“重力量子”。

康普顿效应在康普顿散射中，被散射的光子的波长大于入射光子波长，波长的改变量为

式中， 为光子的散射角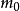， 为电子的静止质量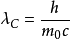， 称为电子的康普顿波长2。

质心系和阈能能量守恒对两个粒子碰撞时所能发生的核反应或事件加上了一个普遍的限制，例如，一个高能光子(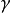 射线)，只有当它的能量超过与电子和正电子的静止质量之和相当的能量时，才能由下列反应产生一个电子-正电子对：

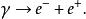因此，对于电子-正电子对的产生，由能量守恒单独规定的阈能或最小能量为

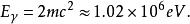正电子的静止质量等于电子的静止质量。

然而，这个反应在自由空间中对于任何能量都是不可能的，因为动量不可能守恒，光子的动量是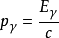。我们选电子-正电子对的质心在其中为静止的参考系来观察这个反应，在这个参考系中，电子动量与正电子动量之和为零：

但在这个参考系中，入射光子的动量并不为零，因为不存在这样一个参考系，在其中能使光子的动量变为零。因此，在质心系中，

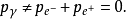由于动量不守恒，反应是不可能发生的，如果这个反应在某个参考系中不可能发生，那么，它在任何参考系中都不可能发生。

这个反应能在另一粒子——例如一个原子核——的附近进行，因为这时原子核可以吸收动量的改变，原子核通过它的库仑场对带电粒子的推和拉，吸收了动量的改变，于是，可能有

核=核+．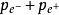

原子核的动量由于反应而改变了，但在其他方面，原子核实际上没有变化，因而它只是起了一种简单的催化剂作用。原子核的初始动量可以是零。

一个重粒子或原子核是吸收多余动量而不吸收很多能量的良好媒介物。这一点可以从非相对论性动能的表达式中看出：

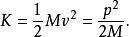也就是，质量M越大，则与给定动量相关联的动能就越小。

本词条内容贡献者为:

李雪梅 - 副教授 - 西南大学