[科普中国]-诺顿定理

诺顿定理(Norton's theorem)：含独立源的线性电阻单口网络N，就端口特性而言，可以等效为一个电流源和电阻的并联。电流源的电流等于单口网络从外部短路时的端口电流isc；电阻R0是单口网络内全部独立源为零值时所得网络N0的等效电阻。

定义诺顿定理（Norton's theorem）指的是一个由电压源及电阻所组成的具有两个端点的电路系统，都可以在电路上等效于由一个理想电流源I与一个电阻R并联的电路。对于单频的交流系统，此定理不只适用于电阻，亦可适用于广义的阻抗。诺顿等效电路是用来描述线性电源与阻抗在某个频率下的等效电路，此等效电路是由一个理想电流源与一个理想阻抗并联所组成的。

诺顿定理是戴维宁定理的一个延伸，于1926年由两人分别提出，他们分别是西门子公司研究员汉斯·梅耶尔（1895年-1980年）及贝尔实验室工程师爱德华·劳笠·诺顿（1898-1983）。实际上梅耶尔是两人中唯一有在这课题上发表过论文的人，但诺顿只在贝尔实验室内部用的一份技术报告上提及过他的发现。

简介诺顿定理与戴维南定理互为对偶的定理。定理指出，一个含有独立电源线性二端网络N(图1a), 就其外部状态而言,可以用一个独立电流源isc和一个松弛二端网络N0的并联组合来等效(图1b)。其中，isc是网络N的短路电流，松弛网络N0是将网络 N中的全部独立电源和所有动态元件上的初始条件置零后得到的网络。上述并联组合称为诺顿等效网络。在复频域中等效网络由电流源Isc和算子阻抗Yi(s)并联而成（图2）。Isc(s)是短路电流的拉普拉斯变换，Yi(s)是松弛网络N0的入端（策动点）导纳。另外，还能导出网络N用于正弦稳态分析和直流分板的等效网络。

求等效电路的关键是求出网络N的短路电流和网络N0的入端（策动点）导纳。它们均可通过电子计算机求得。

isc称为短路电流。Ro称为诺顿电阻，也称为输入电阻或输出电阻。电流源isc和电阻Ro的并联单口，称为单口网络的诺顿等效电路。在端口电压电流采用关联参考方向时，单口的VCR方程可表示为i=u/Ro+ isc1

诺顿定理和戴维南定理是最常用的电路简化方法。由于戴维南定理和诺顿定理都是将有源二端网络等效为电源支路，所以统称为等效电源定理或等效发电机定理2。

证明在单口网络端口上外加电压源u，根据叠加定理，端口电压可以分为两部分组成。分别求出外加电压源单独产生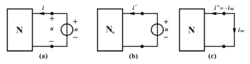的电流i’=u/Ro和单口网络内全部独立源产生的电流i"=-isc，然后相加得到端口电压电流关系式：i=i’ +i”=u/Ro- isc1

注意事项（1）诺顿定理只对外电路等效，对内电路不等效。也就是说，不可应用该定理求出等效电源电动势和内阻之后，又返回来求原电路（即有源二端网络内部电路）的电流和功率。

（2）应用诺顿定理进行分析和计算时，如果待求支路后的有源二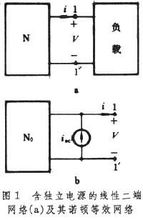端网络仍为复杂电路，可再次运用诺顿定理，直至成为简单电路。

（3）诺顿定理只适用于线性的有源二端网络。如果有源二端网络中含有非线性元件时，则不能应用诺顿定理求解。

诺顿等效电路的计算任何只包含电压源、电流源及电阻的黑箱系统，都可以转换成诺顿等效电路

要计算出等效电路，需：

在AB两端短路（亦即负载电阻为零）的状况下计算输出电流IAB。此为INO。

在AB两端开路（在没有任何往外电流输出，亦即当AB点之间的阻抗无限大）的状况下计算输出电压VAB，此时RNo等于VAB除以INO。

此等效电路是由一个独立电流INO与一个电阻RNO并联所组成。

其中的第2项也可以考虑成：

2a.将原始电路系统中的独立电压源以短路取代，而且将独立电流源以开路取代。

2b.若电路系统中没有非独立电源的话，则RNo为移走所有独立电源后的电阻*****。

转换至戴维宁等效电路左边是诺顿等效电路，右边是戴维宁等效电路，可用下列方程将诺顿等效电路转换成戴维宁等效电路：

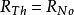
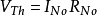
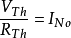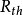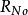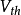其中、、及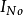分别代表戴维宁等效电阻、诺顿等效电阻、戴维宁等效独立电压源以及诺顿独立电流源。

诺顿等效电路的范例在此范例中，先将A、B两点短路，整体电流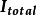可以写成：

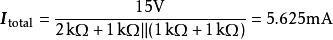
利用电流的分流原则，从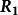流过负载的电流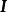为：

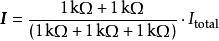
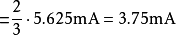
再把电压源用短路来取代，从系统开口两端往里看的等效阻抗为：

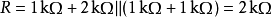
因此，等效电路则是由一个3.75 mA的电流源并联一个2KΩ的电阻所组成。

本词条内容贡献者为:

李雪梅 - 副教授 - 西南大学