[科普中国]-拉格朗日插值公式

拉格朗日插值公式（外文名Lagrange interpolation formula）指的是在节点上给出节点基函数，然后做基函数的线性组合，组合系数为节点函数值的一种插值多项式。

公式简介线性插值也叫两点插值，已知函数y = f (x)在给定互异点x0, x1上的值为y0= f (x0)，y1=f (x1)线性插值就是构造一个一次多项式：P1(x) = ax + b，使它满足条件：P1 (x0) = y0， P1 (x1) = y1

其几何解释就是一条直线，通过已知点A (x0, y0)，B(x1, y1)。

线性插值计算方便、应用很广，但由于它是用直线去代替曲线，因而一般要求[x0, x1]比较小，且f（x）在[x0, x1]上变化比较平稳，否则线性插值的误差可能很大。为了克服这一缺点，有时用简单的曲线去近似地代替复杂的曲线，最简单的曲线是二次曲线，用二次曲线去逼近复杂曲线的情形。1

详细释义任给定F中2n+2个数x1，x2，…，xn+1，y1，y2，…，yn+1，其中x1，x2，…xn+1互不相同，则存在唯一的次数不超过n的多项式pn(x)，满足pn(xi)=y1(i=1，2，…，n+1)，这里：

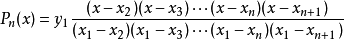叫做拉格朗日插值公式。

公式的几何解释是：存在唯一的次数不超过n的抛物线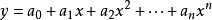

通过平面上的给出的n+1个点M1(x1，y1)，M2(x1，y2)，…，Mn+1(xn+1，yn+1)。

特别地，如对于自变数的两个值，给出了线性函数的(n=1)对应值，这线性函数就被确定。从几何方面说，直线由其两点确定，即：

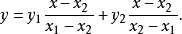
拉格朗日约瑟夫·拉格朗日(Joseph Louis Lagrange)，法国数学家、物理学家。他在数学、力学和天文学三个学科领域中都有历史性的贡献，其中尤以数学方面的成就最为突出。

拉格朗日生平拉格朗日1736年1月25日生于意大利西北部的都灵。父亲是法国陆军骑兵里的一名军官，后由于经商破产，家道中落。据拉格朗日本人回忆，如果幼年是家境富裕，他也就不会作数学研究了，因为父亲一心想把他培养成为一名律师。拉格朗日个人却对法律毫无兴趣。

到了青年时代，在数学家雷维里的教导下，拉格朗日喜爱上了几何学。17岁时，他读了英国天文学家哈雷的介绍牛顿微积分成就的短文《论分析方法的优点》后，感觉到“分析才是自己最热爱的学科”，从此他迷上了数学分析，开始专攻当时迅速发展的数学分析。

18岁时，拉格朗日用意大利语写了第一篇论文，是用牛顿二项式定理处理两函数乘积的高阶微商，他又将论文用拉丁语写出寄给了当时在柏林科学院任职的数学家欧拉。不久后，他获知这一成果早在半个世纪前就被莱布尼兹取得了。这个并不幸运的开端并未使拉格朗日灰心，相反，更坚定了他投身数学分析领域的信心。

1755年拉格朗日19岁时，在探讨数学难题“等周问题”的过程中，他以欧拉的思路和结果为依据，用纯分析的方法求变分极值。第一篇论文“极大和极小的方法研究”，发展了欧拉所开创的变分法，为变分法奠定了理论基础。变分法的创立，使拉格朗日在都灵声名大震，并使他在19岁时就当上了都灵皇家炮兵学校的教授，成为当时欧洲公认的第一流数学家。1756年，受欧拉的举荐，拉格朗日被任命为普鲁士科学院通讯院士。

1764年，法国科学院悬赏征文，要求用万有引力解释月球天平动问题，他的研究获奖。接着又成功地运用微分方程理论和近似解法研究了科学院提出的一个复杂的六体问题(木星的四个卫星的运动问题)，为此又一次于1766年获奖。

1766年德国的腓特烈大帝向拉格朗日发出邀请时说，在“欧洲最大的王”的宫廷中应有“欧洲最大的数学家”。于是他应邀前往柏林，任普鲁士科学院数学部主任，居住达20年之久，开始了他一生科学研究的鼎盛时期。在此期间，他完成了《分析力学》一书，这是牛顿之后的一部重要的经典力学著作。书中运用变分原理和分析的方法，建立起完整和谐的力学体系，使力学分析化了。他在序言中宣称：力学已经成为分析的一个分支。

1783年，拉格朗日的故乡建立了"都灵科学院"，他被任命为名誉院长。1786年腓特烈大帝去世以后，他接受了法王路易十六的邀请，离开柏林，定居巴黎，直至去世。

这期间他参加了巴黎科学院成立的研究法国度量衡统一问题的委员会，并出任法国米制委员会主任。1799年，法国完成统一度量衡工作，制定了被世界公认的长度、面积、体积、质量的单位，拉格朗日为此做出了巨大的努力。

1791年，拉格朗日被选为英国皇家学会会员，又先后在巴黎高等师范学院和巴黎综合工科学校任数学教授。1795年建立了法国最高学术机构——法兰西研究院后，拉格朗日被选为科学院数理委员会主席。此后，他才重新进行研究工作，编写了一批重要著作：《论任意阶数值方程的解法》、《解析函数论》和《函数计算讲义)，总结了那一时期的特别是他自己的一系列研究工作。

1813年4月3日，拿破仑授予他帝国大十字勋章，但此时的拉格朗日已卧床不起，4月11日早晨，拉格朗日逝世。

拉格朗日的科学成就拉格朗日科学研究所涉及的领域极其广泛。他在数学上最突出的贡献是使数学分析与几何与力学脱离开来，使数学的独立性更为清楚，从此数学不再仅仅是其他学科的工具。

拉格朗日总结了18世纪的数学成果，同时又为19世纪的数学研究开辟了道路，堪称法国最杰出的数学大师。同时，他的关于月球运动(三体问题)、行星运动、轨道计算、两个不动中心问题、流体力学等方面的成果，在使天文学力学化、力学分析化上，也起到了历史性的作用，促进了力学和天体力学的进一步发展，成为这些领域的开创性或奠基性研究。

在柏林工作的前十年，拉格朗日把大量时间花在代数方程和超越方程的解法上，作出了有价值的贡献，推动了代数学的发展。他提交给柏林科学院两篇著名的论文：《关于解数值方程》和《关于方程的代数解法的研究》 。把前人解三、四次代数方程的各种解法，总结为一套标准方法，即把方程化为低一次的方程(称辅助方程或预解式)以求解。

他试图寻找五次方程的预解函数，希望这个函数是低于五次的方程的解，但未获得成功。然而，他的思想已蕴含着置换群概念，对后来阿贝尔和伽罗华起到启发性作用，最终解决了高于四次的一般方程为何不能用代数方法求解的问题。因而也可以说拉格朗日是群论的先驱。

在数论方面，拉格朗日也显示出非凡的才能。他对费马提出的许多问题作出了解答。如，一个正整数是不多于4个平方数的和的问题等等，他还证明了圆周率的无理性。这些研究成果丰富了数论的内容。

在《解析函数论》以及他早在1772年的一篇论文中，在为微积分奠定理论基础方面作了独特的尝试，他企图把微分运算归结为代数运算，从而抛弃自牛顿以来一直令人困惑的无穷小量，并想由此出发建立全部分析学。但是由于他没有考虑到无穷级数的收敛性问题，他自以为摆脱了极限概念，其实只是回避了极限概念，并没有能达到他想使微积分代数化、严密化的目的。不过，他用幂级数表示函数的处理方法对分析学的发展产生了影响，成为实变函数论的起点。

拉格朗日也是分析力学的创立者。拉格朗日在其名著《分析力学》中，在总结历史上各种力学基本原理的基础上，发展达朗贝尔、欧拉等人研究成果，引入了势和等势面的概念，进一步把数学分析应用于质点和刚体力学，提出了运用于静力学和动力学的普遍方程，引进广义坐标的概念，建立了拉格朗日方程，把力学体系的运动方程从以力为基本概念的牛顿形式，改变为以能量为基本概念的分析力学形式，奠定了分析力学的基础，为把力学理论推广应用到物理学其他领域开辟了道路。

他还给出刚体在重力作用下，绕旋转对称轴上的定点转动(拉格朗日陀螺)的欧拉动力学方程的解，对三体问题的求解方法有重要贡献，解决了限制性三体运动的定型问题。拉格朗日对流体运动的理论也有重要贡献，提出了描述流体运动的拉格朗日方法。

拉格朗日的研究工作中，约有一半同天体力学有关。他用自己在分析力学中的原理和公式，建立起各类天体的运动方程。在天体运动方程的解法中，拉格朗日发现了三体问题运动方程的五个特解，即拉格朗日平动解。此外，他还研究了彗星和小行星的摄动问题，提出了彗星起源假说等。

近百余年来，数学领域的许多新成就都可以直接或间接地溯源于拉格朗日的工作。所以他在数学史上被认为是对分析数学的发展产生全面影响的数学家之一。2

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学