[科普中国]-顺序主子式

顺序主子式是n阶方阵的n个行列式按顺序排列而成，第k个行列式是由该方阵的前k行和k列组成。对于n阶方阵A，其共有n阶顺序主子式。通过计算方阵A的所有顺序主子式，可以来判断一个实二次型是否正定或方阵A是否为正定矩阵，也可以判断方阵A是否可以进行唯一LU分解。

定义设A为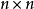 阶矩阵，子式

称为A的i阶顺序主子式。1

对于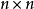 阶的矩阵A，其共有n阶顺序主子式，即矩阵A的顺序主子式由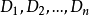共n个行列式按顺序排列而成。

应用判定实二次型正定或矩阵正定

1）实二次型 正定的充分必要条件为A的顺序主子式全大于零。2

2）n阶矩阵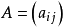 为正定矩阵的充要条件是A的所有顺序主子式 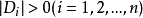。3

根据以上两个定理，可以通过计算矩阵A的所有顺序主子式，来判断一个实二次型是否正定或矩阵A是否为正定矩阵。

判定矩阵是否可唯一LU分解

设矩阵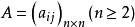 的各阶顺序主子式Di（i=1,2...n-1)不等于0，则A有唯一LU分解

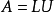
其中，L为单位下三角矩阵，U为上三角矩阵。4

根据以上定理，可以通过计算矩阵A的所有顺序主子式，来判断矩阵A是否可以进行LU分解，且为唯一分解。

举例设阶矩阵

则A的顺序主子式为：

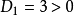
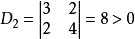
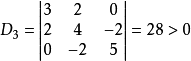
所以A是正定的，由其构成的实二次型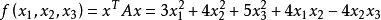是正定的。

因为A的各阶顺序主子式均不等于0，所以A有唯一LU分解，分解结果如下（）：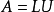

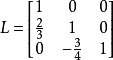
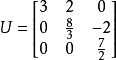
本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学