[科普中国]-惩罚函数

惩罚函数亦称处罚函数，是一类制约函数。对于约束非线性规划它的制约函数称为惩罚函数，其中的 M 叫惩罚因子（或罚参数）。

简介惩罚函数亦称处罚函数。一类制约函数。

对于约束非线性规划问题

它的形如

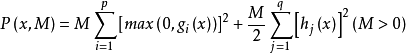的制约函数称为惩罚函数，其中的 M 叫惩罚因子（或罚参数）。1

外点法(exterior point method)

外点法亦称惩罚函数法或外惩罚函数法。将求解约束非线性规划问题转化为求解一系列无约束极小化问题的一类制约函数法。

对于约束非线性规划问题(NP)求解过程如下：选取一系列递增的惩罚因子 Mk(k=1,2,...) ，作相应惩罚函数列：

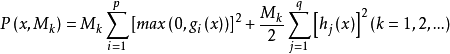将求解问题(NP)转化为求解一系列无约束极小化问题

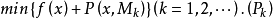
设 xk是 (Pk) 的最优解，则在一定条件下可以证明点列 {xk} 存在极限点 x* ，并且 x* 是问题 (NP) 的最优解。用此法求解 (NP) 是将“惩罚”加于不可行点，通过逐步增大惩罚因子Mk，迫使解的迭代点列 {xk} 从可行域外部向位于可行域边界上的某最优解接近，所以称为外点法。由于利用了惩罚函数进行求解，故也称惩罚函数法或外惩罚函数法。

外点法的经济解释是：一个采购者的经济决策问题，即如果把目标函数视为采购者决策时要花费的总“价格”数，约束条件视为某种“规定”，采购者在“规定”范围内买东西不罚款；若违反“规定”，则按罚款政策罚款。因此，采购者付出的总代价应是总的“价格”数与总的罚款数之和，采购者要以总代价作为最终目标。当把罚款政策定得非常苛刻时，即违反“规定”，则重罚，迫使采购者做决策时不敢违反“规定”，否则，他的总代价就不可能省。在数学上则表现在惩罚因子 M* 足够大时，无约束极小化问题的最优解 x* 应该满足诸约束条件，因而是约束极小化问题的最优解。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学