[科普中国]-熔化曲线

晶体温度随时间的熔化曲线，从不断增大到熔化阶段的不随时间变化。在过渡的地方教材中是用了光滑曲线连接的。如果用不同酒精灯加热就会发现，用的酒精灯越多，熔化曲线约平滑，而酒精灯越少（小），拐的弯越明显。那么可以认为，在无限缓慢加热的理想状况下，就会是一个折线了。

实验利用壳层模型分子动力学方法，研究了高温高压条件下FeO的熔化温度，同时还计算了温度在300K及压强上升到140GPa时FeO的状态方程。作者在研究中，考虑了分子动力学模拟熔化存在的过热现象，通过晶体的现代熔化理论，对FeO的分子动力学模拟熔化温度进行了修正，获得了高温高压下FeO正确的熔化温度。图此，为常压下利用壳层模型分子动力学研究物质熔化提供了一种较好的方法，该方法亦可进一步推广应用到其它物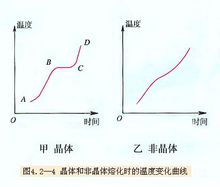质的高压熔化研究）工作。

典型金属高压熔化曲线的研究熔化是一种常见的相变。熔化温度一般随压力的改变而改变，固体熔化温度与压力的关系在材料科学、高压物理以及地球物理等领域有着重要的应用价值。以金属元素为研究对象，通过理论计算和实验两种途径对金属的高压熔化曲线进行了初步的研究。1

高压熔化的自由体积理论Lindemann熔化定律的物理图像非常直观，是一种对熔化时晶体结构不稳定性的直观理解。Martin和Luo对该定律的假设进行了检验。artin等用布拉格散射技术测量了AL，Cu和几种碱金属卤化物晶体在熔点附近的δ值，发现δ的确随着温度的升高而变大，并且δ达到一定程度时晶体熔化，但该实验仅仅测量了常压下的数据，只是部分验证了Lindemann熔化定律的假设。2005年，Luo用分子动力学方法模拟了Lennard-Jones（LJ）势能的系统，发现随着压力的增大δ并不是常数，其随压力的变化是不可忽略的，在常压和极端压力下，δ分别为0.116和0.145，极端压力下比常压下大出约30%，可见不管是用Lindemann熔化定律的假设δ二常数还是利用其自由体积形式VfV=const来计算熔化曲线，都将会造成很大的误差。为了得到比较精确的熔化曲线，必须对δ或Vf随压力变化的规律有准确的描述，对于加压时发生固固相变的材料，还要对常压相和高压相分段计算熔化曲线。1

计算细节与计算结果先计算了Al，Cu，Ni金属的熔化曲线，Al，Cu，Ni 在常压下为fcc结构，在所研究的温度和压力范围没有发现固固相变，这是一类最简单的情况。利用计算得到的熔点处的自由体积，拟合出这三种材料的参数a，b的值。然后计算相应材料的熔化曲线，也列出了其他文献报道的数据，同时也将按照VfV=const计算得到的熔化曲线列出作为对比。

按照计算得到的结果与其他文献中报道的数据符合的很好，而按照原假设VfV=const计算得到的结果随着压力的增大与其他文献中报道的数据相差甚远，这说明方法是行之有效的，在高压下材料不满足VfV=const这个假设，该假设只在很低的压力下近似成立，在研究中由于不涉及很高的压力，因此可以使用该假设计算熔化曲线，当研究的压力范围拓展至更高压力时，必须对该假设进行修正。1

计算Na和K的熔化曲线要复杂一些。它们在高压下会发生固固相变，并且Na还存在着反常熔化现象。对于Na这类有反常熔化现象的材料，没有成熟的计算方法，一般是采用Kechin方程拟合实验值得到熔化曲线。对于这类材料方法依然有效，将常压相和高压相分开计算。计算Na的熔化曲线时，采用常压熔点、熔化温度最高点、以及bcc-fcc液态三相点这三个点的自由体积数据来确定参数，以确保熔化曲线通过三相点。对于高压相的熔化曲线，以三相点为起点来计算。K熔化曲线的计算与Na类似，常压相熔化曲线的计算采用常压熔点、压力中间点·三相点这三个点的自由体积数据确定参数a，b的值。同时我们也按照VfV=const计算了相应的熔化曲线作为对比。1

HfC熔化曲线的第一性原理分子动力学采用第一性原理分子动力学Z方法计算HfC在高压下的熔点，改变超胞体积，计算得到了HfC在三种压力下的熔点值，熔点分别为3638.01K、3723.52K、3730.05K，对应压力为12.68GPa、15.89GPa、20.93GPa。拟合得到随压力变化的熔化曲线，低压时HfC熔点随压力变化快，而高压时熔点变化很小；常压时HfC的计算熔点约为3300K。2

参数设置采用基于第一性原理的软件VASP对HfC在高温高压下的熔化曲线进行分子动力学模拟。离子实与价电子之间的相互作用采用全电子投影缀加波（PAW）方法表示，交换关联作用采用广义梯度近似（GGA）的Perdew-Burke-Emzerhof（PBE）形式，平面波截断能采用默认的最大值。在模拟中，采用微正则系综（NVE），超胞中粒子数目、体积和能量保持不变。时间步长为1fs，总的模拟步数为4000步。HfC超胞结构共含有64个原子，包括32个Hf原子和32个C原子。2

HfC 的熔化过程采用分子动力学Z方法计算HfC的熔点时，首先建立HfC的超胞结构，超胞由2×2×2倍的晶胞组成，共含有64个原子，采用周期性边界条件。为了得到不同压力下的熔点，改变初始超胞的晶格大小，超胞体积分别为：809.558Å3、799.179Å3和778.688Å3。

对于熔化的发生，解释如下：分子动力学Z方法中采用NVE系综，超胞中粒子数、体积、总能在模拟过程中保持不变，即HfC在熔化前后总的Gibbs自由能相等：Gsolid(V，TLS)=G(V，Tm)；当到达一定过热温度时，若继续升温将导致材料熔化；HfC 发生熔化时，由于熵显著增加，为了保持体系能量不变，则温度必然降低，在熔点处（低于过热温度）达到平衡稳定。2

HfC的熔化曲线为了得到HfC的熔化曲线，选取了3种超胞结构体积，体积分别为809.558Å3、799.179Å3和778.688Å3。采用分子动力学Z方法计算得到HfC在不同压力下的熔点值，熔点分别为3638.01K、3723.52K、3730.05K，对应压力为12.68GPa、15.8GPa和20.93GPa。

HfC的熔化曲线表示HfC熔点随压力的变化规律。在压力低于15.89GPa时，压力升高，熔点增大，斜率为26.64K/GPa。当压力大于15.89GPa时，压力升高，熔点变化很小，斜率只有1.30K/GPa，变化幅度明显小于低压时。在常压下，HfC的熔点约为3300K。2

本词条内容贡献者为:

张磊 - 副教授 - 西南大学