[科普中国]-激光与生物组织相互作用

激光与生物组织相互作用，分为可逆的作用和不可逆的作用两种情况。

激光作用于生物组织发生可逆反应的情况下，包含了多种相互作用，包括散射、吸收、反射等。不同的生物组织由于其光学特性的不同，对激光作用的应答性反应也会不同。在组织的光学特性中，最重要的是反射、吸收及散射系数，它们共同决定了某一波长的光在组织中的传输情况，而“组织光学”（Tissue Optics）正是基于此研究领域发展起来的，是研究光辐射能量在生物组织体内的规律以及有关组织光学特性的测量方法的一门新兴交叉学科。

不可逆的作用则主要分为5种类型：光化作用（photochemical interaction），热相互作用（thermal interaction），光蚀除（photoablation），等离子体诱导蚀除（plasma-induced ablation）和光致破裂（photodisruption）。基于此方面的研究则主要用于疾病的治疗。

1.激光与生物组织发生可逆相互作用1.1光学特性的基本原理光在传播过程中碰到物质会发生的现象包括反射、折射、散射和吸收。图1为光束入射薄片物质上的一些典型情况。

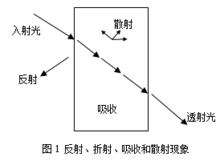
图1 反射、折射、吸收和散射现象

1.2 组织中光传输目前研究光在生物组织中的传输主要有两种理论：电磁理论和辐射传输理论。电磁理论以麦克斯韦方程为基础，考虑介质的统计特性及光的波动性，从原理上讲它是最基本的方法，包含所有的衍射效应；其不足之处在于数学上过于复杂，使其在实际应用中受到限制，唯有在微米尺度上研究组织散射特性时有所应用。辐射传输理论不直接从麦克斯韦方程出发，它忽略了光的波动性和生物组织的内在结构，直接处理了光能量在生物组织内的统计传输过程，虽然其缺乏电磁理论的严格性，但它有着良好的实验基础，适合绝大多数的光传输问题，因而在组织光学内得到了广泛的应用。

在辐射传输理论中，生物组织被抽象成是一个由大量吸收和散射元的集合。这些吸收和散射元服从统计均匀分布，同时还忽略了光的波动性，仅考虑光能量在组织内的传输过程。此时，利用辐射传输理论得到的方程可以较好的描述光子及其携带的能量在生物组织内的统计平均传输过程。

一般情况下，辐射传输方程无法得到解析解，因此该理论也发展了多种近似理论和数值算法，分为级数展开，离散求解，随机模型三类，分别以漫射近似理论、Kubelka-Munk理论和Beer-Lambert定律、蒙特卡罗方法和随机游走理论为代表。上述方法都是在给定初始值和特定边界条件基础上建立起来得，因此都有特定的适用条件。这里，我们简单介绍其中两种方法，蒙特卡罗模拟（Monte Carlo simulation）和Kubelka-Munk理论。

1.2.1 蒙特卡罗模拟

蒙特卡罗方法以光子的随机行走模型来模拟光在生物组织中的传输，理论上可以处理任何条件下的光传输问题，被认为是最接近实际的方法。早在1978年，Meier就提出了蒙特卡罗模型，并将蒙特卡罗方法引入了组织光学进行生物组织光传输问题的研究，在其后数十年，基于蒙特卡罗方法的研究已取得了巨大的成果。

蒙特卡罗模拟的基本思想是：应用吸收和散射现象来跟踪光子通过混浊介质的光程。将光子两次碰撞之间的距离设置为对数分布，用计算机产生的随机数表示，通过对每个光子确定一个权值，并且在传播过程中持续的减小权值来表示吸收现象。如果发生散射，则由给定的相函数和一个随机数来确定一个新的传播方向。当光子逃逸出组织模型或其权值低于某一确定阈值时，定义光子消亡，模拟过程结束。根据Meier的观点，蒙特卡罗模拟主要由五个步骤组成：源光子的产生（source photon generation），轨迹的产生（pathway generation），吸收（absorption），消亡（elimination）和检测（detection）。

为了克服蒙特卡罗模型计算量大的难题，1993年，R.Graaff和M.H.Koelink等提出了精简的蒙特卡罗模型，即用一组光学参数(散射系数、吸收系数、各向异性因子)的模拟，推知其他参数条件下的光传输规律，这样可节省了重复计算所需的大量时间。

1.2.2 Kubelka-Munk理论

Kubelka-Munk理论是由Kubelka和Munk提出的，局限于线性几何的一种模型，它的参数通常用于医学物理领域。Kubelka-Munk理论仅能处理漫射辐射，并且局限于散射远远超过吸收的情况。

理论的假设前提是，辐射度完全是由漫射得到的，即Jc=0。图2描述了在生物组织内可被区别的两个漫射光通量的几何图形。在辐射光入射方向上的光通量为J1，在相反方向上后向散射的光通量为J2。

图2 Kubelka-Munk理论两个通量的几何图

有两个Kubelka-Munk理论系数，AKM和SKM，它们分别被定义为吸收和散射漫射辐射。应用这些参数，可得到两个微分方程：

式中，z代表的是入射辐射的平均方向。方程（1）和（2）通解可表示为：

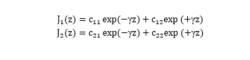
其中，，Kubelka-Munk理论中最重要的问题是怎样用来表示和。

Kubelka-Munk理论是一种被称为多通量理论的特殊形式。在这个理论中，当考虑到在许多离散角上的辐射度时，传输方程就变成一个矩阵微分方程。除了Kubelka和Munk提到的两个方向上的通量外，在其他理论中还涉及到更多的光通量，但所有这些多通量理论，都局限于一维几何结构，并且假设入射光已被漫射，同时它的计算量也非常大。

2. 激光与生物组织发生不可逆相互作用激光与组织不可逆的相互作用主要被分为5种类型：光化作用（photochemical interaction），热相互作用（thermal interaction），光蚀除（photoablation），等离子体诱导蚀除（plasma-induced ablation），光致破裂（photodisruption）。

2.1光化作用光化作用，即大分子或是生物组织内，光可以引起化学作用和化学反应，比如光合作用引起的能量的释放。在激光医学物理领域的光动力学疗法（photodynamic therapy）中，光学作用机理起着很重要的作用。

在低功率密度（典型功率为0.01~50W/cm）和长时间曝光下（秒以上或者连续照射），光化作用就会发生。在多数实例中，普遍选择波长在可见光范围内的激光器，因为其具有较高的发光效率和高的光穿透深度。

2.2热相互作用光热作用主要是组织吸收激光能量后转为为热能，导致组织温度升高，根据组织的不同反应，可以分为凝结、汽化、碳化和熔融，主要应用于治疗视网膜脱落 ，激光诱导间质热疗法等。

热产生是由激光参数和生物组织的光学性质决定的。这些性质主要是指辐照度、曝光时间及吸收系数。这里采用的典型脉冲持续时间为1微秒至1分钟，典型功率密度为10~10W/cm。热传输完全由热导率和热容量等生物组织热血特性表征。热效应最终依赖于生物组织的类型和生物组织内所达到的温度。

2.3 光蚀除作用光蚀除是当某种材料在高强度激光的照射下，产生分离的现象。光蚀除作用的物理原理是组织吸收高能量的紫外的光子，然后被提高到互相排斥的激发态，这时共价键离解，而组织不坏死，这样就达到了蚀除的目的。它的优点是切割的精准性、极好的可预测性和对邻近组织的无热损伤性。它的脉冲持续时间是10~100ns，典型的功率密度是10至10W/cm。

2.4 等离子体诱导蚀除当固体和流体得到超过10W/cm功率密度，或气体得到10W/cm的功率密度时，就会发生光击穿现象。当激光参数选取合适时，用等离子体诱导蚀除法，就可以得到光滑的、轮廓清晰的组织分离，而不会产生任何热损伤或机械损伤。等离子体诱导蚀除也被称为等离子体传递分离。典型脉冲持续时间为100fs~500ps，而功率密度范围为10—10W/cm。等离子体诱导蚀除主要应用于角膜屈光手术。

2.5光致破裂当脉冲能量很高时，冲击波和其他机械方面的影响就变得很重要，这就导致了一种新的作用—光致破裂。与光致破裂作用有关的物理效应是等离子体的形成和冲击波的产生。它将激光能量转换成机械能而产生高冲击力的冲击波，这种冲击波靠其强有力的冲击力来粉碎组织。

光致破裂的主要决定因素是激光峰值功率、脉冲宽度、脉冲强度以及激光光束的聚焦程度，可通过调节这些参数来获得预期结果。一般情况下，脉冲持续时间为100fs~100ns，典型功率密度为10—10W/cm。光致破裂最主要的应用是晶状体切开术，同时还可以用于泌尿系统结石的激光诱导碎石术中。

扩展阅读[1] 谢树森，雷仕湛.2004.光子技术.北京：科学出版社

[2] 姚翠萍，张镇西.1999.激光与组织的相互作用.激光生物学报，8（2）：102~108

[3] 张镇西. 2008. 生物医学光子学新技术及应用.北京：科学出版社

[4] Ascher P W, Justich E, Schroettner O. 1991. A new surgical but less invasive treatment of central brain tumours. Acta Neurochir, 52:78~80

[5] Boulnois J L. 1986. Photophysical processes in recent medical laser development: a review. Laser in Medical Science, 1:47~66

[6] Graaff R, Koelin M H, de Mul F F M, et al. 1993, Condensed Monte Carlo simulations for the description of light transport. Applied Optics, (32): 426~434

[7] Hale G M, Querry M R, 1973. Optical constants of water in the 200nm to 200wavelength region. Applied Optics, 12:555~563

[8] Niemz M H, Loesel F H, Fischer M, et al. 1994. Surface ablation of corneal tissue using UV, green and IR picosecond laser pulses. Proceeding of SPIE, 2079:131~139

[9] Neimz M H. 2005. 激光与生物组织的相互作用——原理及应用（第三版）.张镇西等译.北京：科学出版社

[10] Parsa P, Jacques S L, Nishioka N S. 1989. Optical properties of rat lver btween 350 and 2200 nm. Applied Optics,28:2318~2324

[11] Wang L H,Jacques S J,1995. Monte Carlo modeling of light transport in multi-layered tissues. University of Texas M D Anderson Cancer Center. Computer methods and Programs in Biomedicine, 47（10）：131~146

[12] Yooh G, Welch A J, Motamedi M, et al. 1987. Development and application of three-dimensional light distribution model for laser irradiated tissue. IEEE Journal of Quantum Electronics, 23(2):1721~1733

本词条内容贡献者为:

张镇西 - 教授 - 西安交通大学