[科普中国]-反应曲面法

说明

反应曲面法在协助研究人员对科学系统或工业制程中最佳产品设计、制程改善、系统最佳化等问题提供一套分析、求解程序，大部分应用时机均属工业性研究，尤其是当系统特性受大量变数影响状况下最为适当。1

历史

|| || 表1.反应曲面法的发展历史

概念反应曲面法之研究问题，一般假设问题为限制性之最佳化问题，目标函数的确切型式是未知的 ， 为误差，反应曲面法一般在此前提的假设与应用系统的限制下，可有效地求得最佳实验或作业变数值。 一般来说，执行反应曲面法大致分为两阶段:

第一阶段称为反应曲面设计(response surface design)；

第二阶段称为反应曲面最佳化(response surface optimization)。2

反应曲面设计为探讨独立变数与反应变数之间的数学模式关系，因此欲对于反应和独立变数之间找出一个适当的近似函数。通常利用独立变数在一些范围里的低阶多项式近似，即为一阶回归模型 (first-order model)：

如果系统中有曲率，则必须利用较高阶的多项式，如二阶模型(second-order model)：

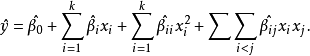获得最适化实务模型便是本阶段最重要的议题。收集资料后以最小平方法 (least squares estimation, LSE) 配适，以寻找出一个适当近似的函数，采用回归分析的显著性检定 (general linear test approach) 来了解独立变数与反应变数间的关系强弱，并检定配适的模式是否恰当 (statistical adequacy)。当实验区域接近最佳反应值附近时，真实反应曲面的曲率 （curvature） 会增加，则考虑二阶模型，同样的，我们需要检定二阶模式的适当性。当这个二阶回归模式配适良好时，便可以利用这二阶模式求得最适操作点及特征化反应曲面。

反应曲面最佳化反应曲面法是一个逐次的程序(sequential procedure)。通常，当我们是在反应曲面的一个远离最佳状况的点时，系统只有少量的曲率而一阶模型会是适当的，在此欲沿着改善路径快速且有效地朝向最佳点 (optimum) 附近。

进而利用最陡上升(下降)法 (steepest ascent/descent method)。所配适一阶模型的反应曲面，也就是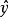 的等高线，沿着最大反应变数增加(减少)逐次移动程序，直到反应值无法再改善为止，其中，前进步伐的决定并非固定不变，可以根据实验情况或经验值决定，接着以此组操作水准为新的实验中心点，并重复实验步骤，往最佳反应曲面的方向逼近，并且执行线性模式之缺适性检定，一旦发现一阶回归模型不适合时，表示已接近最佳点，此时应采用更复杂的数学模式来进行分析。

如果选择二阶模式配适实验资料时，一般进行中央合成设计实验 (central composite design，CCD)或是三水准因子设计 (three-level factorial design)，在配适及检定二阶模型完成之后，就进行反应曲面分析，指在目前实验区域中，以实际不同情况(或制程限制)针对反应曲面系统作深入探讨。此时可利用正规分析或脊线分析等技术来进一步了解稳定点 (stationary point) 之数学特性，其发现为鞍点(saddle point) 则需进行更进一步的脊线分析，并配合反应曲面图(或轮廓图)的协助，若二阶模式配适时仍存在缺适性之问题，则可以求得局部最佳操作状态或再进而配适更高之回归模式，如三次 (cubic) 或四次 (quartic) 模型。

优点经济性原则：反应曲面法可以使用部分因子设计或特殊反应曲面设计（如混种设计等 （hybrid design）），以较少的实验成本及时间获得不错且有效的资讯。

深入探讨因子间交互作用影响：反应曲面法可以经由分析与配适模式来研究因子间的交互作用，并且进而讨论多因子对反应变数影响的程度。

获得最适化的条件：根据数学理论求得最适的实验情况，同时利用配适反应方程式绘出模式三度空间曲面图与等高线图，观察并分析出最适的操作条件。

减少模拟时间：可获得模拟独立变数与反应变数关系之数学模型，借此将实验次数及时间降低。

限制在应用上主要存在下列二项限制：

只适用于连续性的系统，是假设所有反应值与独立变数的量测刻度是连续性的。

影响系统之独立变数(可控制和不可控制变数)是属于计量性。3