[科普中国]-极小曲面

平均曲率为零的曲面。平均曲率定义为：其中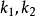 表示两个主曲率。给定一条闭曲线，可以设想蒙在这条闭曲线上的所有曲面中，有一个面积最小者，这个具有最小面积的曲面正是极小曲面。平面是仅有的极小可展曲面。除平面外，旋转极小曲面都是悬链面，直纹极小曲面都是正螺面。

极小曲面的经典例子包括：

1）欧几里得平面，无特别约束条件下最平常的极小曲面；

2）悬链曲面：由悬链线围绕其水平准线旋转而得到的曲面。这是最早发现的“不寻常”的极小曲面。悬链曲面状的皂液膜可以由将两个等大的圆环紧贴放入肥皂水中，拿出后再缓慢分开得到；

3）螺旋曲面：一个线段沿着垂直于其中点的直线匀速螺旋上升时扫过的曲面。这是继悬链曲面后发现的第二种不寻常的极小曲面；

4）恩内佩尔曲面。

给定一个嵌入曲面，或更一般的，一个浸入曲面（其边界一般固定，但不一定有界），定义其平均曲率如下：

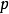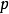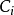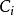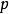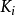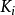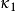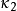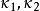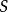令 是曲面 上一点，考虑 上过 的所有曲线 。每条这样的 在 点有一个伴随的曲率 。在这些曲率 中，至少有一个极大值 与极小值 ，这两个曲率 称为 的主曲率。

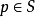的平均曲率是两个主曲率的平均值，由欧拉公式其实也是所有曲率的平均值，故有此名。

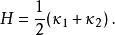而极小曲面是指每一点上的平均曲率都是0的曲面。这种曲面的研究始于有关满足一定的约束条件（比如边界固定或容纳体积满足一定条件）下表面积最小的曲面，因此被称为“极小曲面”。实际上极小曲面所囊括的内涵比此类最小面积曲面更广泛。极小曲面的定义还可以扩展到恒定平均曲率曲面，即曲面上由平均曲率等于某个常数的点组成的子曲面。当这个常数等于零的时候， 恒定平均曲率曲面就是极小曲面。极小曲面是平均曲率流的临界点1。

极小曲面上的布朗过程可以用于某些极小曲面相关定理的概率证明。

著名的普拉托实验是把围成封闭曲线的金属丝放入肥皂溶液中，然后取出来，由于表面张力的作用，在它上面就蒙有表面积最小的薄膜。这种表面积最小的曲面就是所谓极小曲面，从数学上求这膜曲面的问题称为普拉托问题。这个问题可以用变分法来解2。

从变分学观点看，可以考虑以已知闭曲线Γ为固定边界的曲面的法向变分。由欧拉-拉格朗日方程(见变分法)，对于任何这样的变分,曲面面积达到临界值的充要条件是曲面的平均曲率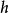为0。因此，通常就用这个几何条件来定义极小曲面。

在三维欧氏空间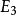中，若一张曲面可用方程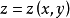来表示，则称它为图，或非参数化曲面。由极小条件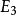，中极小图的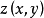满足下述二阶非线性椭圆型微分方程：

通常称它为极小曲面方程。