[科普中国]-细长体理论

细长体理论的假定

每个截面上的横向流动与其它截面上的流动无关；

描述方程如右图所示；

上述简化是由蒙克（Munk）在论述飞艇理论时首先引入，然后由琼斯（R.J.Jones）推广到任意马赫数时任意横截面的细长体上。

简化所依据的基本物理概念对极细长的物体，至少在物体附近，x方向的参数变化比其余方向小得多，更明确的说，就是假定，省略项与其余项相比可以忽略不计。

描述方程的求解简化之后的描述方程与描述平面不可压缩流动的方程相同，对它可以采用一般的保角映射法进行求解。上述二维流动与实际的三维问题之间通过边界条件相关联。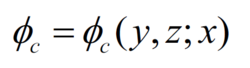

描述方程解的形式为如右图所示；其中以x作为参数，它相当于在每个截面上边界条件都是x的函数，这是由于边界条件依赖于物体几何形状的缘故。

工程应用根据细长体理论，某个给定物体的升力系数只依赖于横向流动，因此与总的流动马赫数无直接关系。对于实际应用来说，此理论的精度较低。它的用处在于普遍性。对于复杂形状的细长体，它可以提供最好的升力估算方法。

简单的横向流动理论不能给出正确的厚度阻力，因为厚度阻力含有与物体不同截面之间相互作用有关的项，所以用于阻力的一般细长体理论就不像用于升力那样简单。科尔（Cole）利用适当的细长比小参数，给出了系统的级数展开式，他给出了展开式中依次各项的量级讨论并估计了准确度，提供了合理的拓展方法，即保留高阶（非线性）项，对精确运动方程的解作逐次近似。2