[科普中国]-地心纬度

为了便于计算和绘图，通过大地测量推得多种近似于大地水准面的椭球面，作为地球形状的数学模型，并称为参考椭球1。

地心纬度为参考椭球上一观测点和椭球中心的连线与赤道平面之间的夹角。

右图是一个子午面（过观测点和地轴的参考椭球截面）。O是地心，x轴在子午面内，y轴指向北极。M是参考椭球上的任意一点，Mn垂直于参考椭球表面，即Mn是参考椭球表面的一条法线。

就是地心纬度（Geocentric Latitude），它是地心垂线MO与赤道平面的夹角。

另外两个角度分别是：

是地理纬度（Geographic Latitude），它是法线Mn与赤道平面的夹角。

是归化纬度（Reduced Latitude），它是M'O与赤道面的夹角。M'M垂直于x轴，且M'O的长度等于地球长半轴。

设参考椭球方程为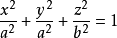：（其中a为长半径，b为短半径）

1）地心纬度与归化纬度的关系

如右图和简介中的右图可得，点M的坐标为（L为经度），将x和y带入参考椭球方程可得。

由点M的x和y坐标可知纬线半径，由此可得到点M所在的子午椭圆的表达式为：

对于地心纬度和地心半径有：。

所以。

2)地心纬度与地理纬度的关系

为方便起见，取L=0的起始子午面，则点M的坐标为：

又由右图可得到起始子午圈上点M切线的斜率为

微分得

即，由1）中可知。2

由于经线的曲率自赤道向两极减少，一个地方的地心纬度总不大于它的地理纬度，特别在南北纬45°的地方，在那里，二者的差值达11'.5之多。

自赤道到南北纬45°，地心纬度始终小于地理纬度，而且，二者的差值随着纬度的增高而增加；自南北纬45°到南北两极，地心纬度仍旧小于地理纬度，但二者的差值随纬度的增加而减小。3