[科普中国]-散射矩阵

概念阐释定义

假设散射源为很好的定域散射源，与被散射粒子的相互作用局限在有限的空间范围内，那么，无穷远时间以前粒子处于一个自由态，称为入态，记为|Ψ>in；无穷远时间之后粒子也是处于一个自由态，称为出态，记为 |Ψ>out。 入态到初态，相互作用可以用一个矩阵描述，记为S，那么就有：

|Ψ>out=S |Ψ>in

这就是散射矩阵的定义。现代高能物理的发展，同其他物理学一样是理论和实验的互动，而这种互动主要的桥梁就是散射矩阵。

散射矩阵直接与可观测的物理量相联系，但是我们在量子场论中处理的是场，利用一个LSZ约化规则，它联系了量子场论中的格林函数和可观测的散射矩阵。这使得理论能够预言实验。

在微波元件中的定义散射矩阵在微波元件中表示网络特性的参量之一，在n端口线性网络中，描述各端口归一化入射电压波a与归一化反射电压波b之间的关系为[b]=[S][a]，其中[S]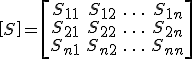称为散射矩阵，各矩阵元素Sij称为散射参量，其优点是在微波网络中便于测量，且有

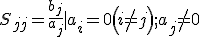
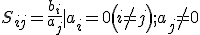
Sjj和Sij分别表示除第j端口接信号源其余端口全部接匹配负载时，第j端口的归一化电压反射系数和从第j端口到第i端口的归一化电压传输系数。

两种极化散射矩阵辛克莱散射矩阵在雷达目标散射问题中, 散射矩阵完整地体现了人射电磁场矢量与散射电磁场矢量之间的关系。实际系统中, 入射电磁场来源干雷达发射机, 而散射电磁场则由雷达目标散射产生并为雷达接收机所接收。我们知道, 散射矩阵的确定与收发系统的配置无关, 因此它包含的仅是雷达目标的信息, 体现的仅是雷达目标的特性。

由于任意雷达目标的散射矩阵都可以通过测量得到, 所以通过研究各种目标的散射矩阵就可得到这些目标的散射特性。现有的研究成果表明, 雷达目标的横截面积对于入射电磁场的极化状态是很敏感的, 我们可以将任何目标均视为一个极化变换器, 而散射矩阵正好描述了该目标的极化变换特性。

如果用[S] SMA 表示含绝对相位的辛克莱散射矩阵, 用[S]SMA表示含相对相位的辛克莱散射矩阵, 则1

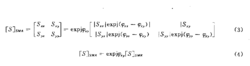
米勒散射矩阵当我们用斯托克斯( S ot k e s )矢量来描述电磁波的极化状态时, 目标的极化散射矩阵为米勒矩阵。此时雷达目标的极化变换效应可用性4*4 在米勒矩阵来加以描述, 值得注意, 该矩阵的所有阵元均为实数

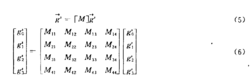
我们根据描述入射场极化矢量与散射场极化矢量之间关系的辛克莱散射矩阵[S]可以求得米勒矩阵的各个实阵元。我们知道斯托克斯矢量与极化矢量之间存在关系

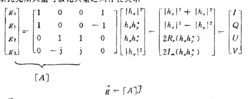
即可得到米勒矩阵[M]与辛克莱矩阵[S]之间的关系式1

测量方法通常极化散射矩阵的测量是利用专用的测量雷达，分时测量得到的。

目前方法一是利用专用的极化测量雷达，在两个正交极化通道上，同时发射两个正交极化Ex、Ey，(如果Ex=Ey，其合成矢量就是一个夹角为45°的线极化)，然后，通过信号编码的方法，来完成极化矩阵的“同时性”测量。其成功之处在于解决了极化测量雷达的两大问题。一是打破了快速极化开关给测量精度度带来的误差；二是消除了由转换开关造成的脉间相位和幅度的不稳定性所带来的误差。

但是，这种测量方法不可避免的存在两个小小的不足：①同时发射的Ex、Ey，在空间合成后，乃至入射到目标上，它仍是一个斜线极化波，因此所得到的散矩阵实际上是一个由线极化入射产生的、极化基旋转了45 °后的变换矩阵而已，它得不到完整散射特性。②它需要专门的测量雷达。由于极化信息处理利用日益广泛，往往要求在值班极化雷达上，对目标散射矩阵进行在线实时测量，而不是另加测量雷达。2

方法二是利用相对极化矩阵的测量框图及其原理，但测量方法仍是分时进行的。由于目标通常指运动目标，散射矩阵随目标姿态变化而变化，这就要求我们对散射矩阵进行实时测量，才能达到欲完成的控制目的。正是基于这种考虑，利用正在值班(担负任务)的极化捷变雷达，对散射矩阵进行实时测量，是本文的贡献。归纳起来讲，①利用正在值班的极化雷达，而不是另配极化测量雷达；②对散射矩阵进行实时测量，以达到实时控制的目的。2