[科普中国]-引力透镜效应

产生原因

引力透镜是强引力场中一种特殊的光学效应。假设地球与一颗遥远的天体之间刚好有一个强引力场天体，三者差不多在一条直线上，强引力场天体附近的时空弯曲使远方天体的光不能沿直线到达地球，而使地球上观测到的像偏离了它原本所在的方向，其效果类似于透镜对光线的折射作用，称为引力透镜效应。早在1911年爱因斯坦即提出远方恒星的光线掠过太阳表面时会发生微小的偏转，1919年5月25日英国天文学家爱丁顿率领的观测队在非洲普林西比岛通过日全食观测验证了这一结果。这是引力透镜效应的最初概念。产生引力透镜效应的中间天体叫做前置天体。这一效应可能产生双重像或多重像，这些像有相同的光谱结构和谱线位移量。特殊情况下，远方天体的像会形成环状(爱因斯坦环)1。

物理原理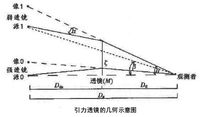

最简单的模型为光线经过一大质量质点时发生偏折的情况，如上图。在这种情况下，假设光子的瞄准距离为b，质点质量为M，则由牛顿力学可得光子的横向加速度为：

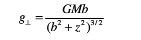
横向方向的速度为：

因此光线的偏折角为：

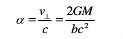
这是牛顿力学得到的光线偏折角，而在广义相对论的修正下，偏折角应为上式的两倍，即：

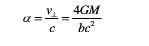
以质点为前提的光线偏折其结果虽然简单，但其讨论过于粗糙。而更一般的情形是非质点条件下的光线偏折。对于质量分布为ρ（ξ1ξ2ξ3）的延展透镜体，由于透镜到观测者和源的距离都远远大于透镜本身的厚度，因而在计算时可将透镜作平面近似，将之视为二维平面。因此，总偏转角等于各质元偏转角的矢量和：

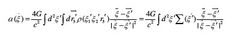
其中定义为体质量密度沿径向（光线方向γ3）积分后的面质量密度，（ξ1，ξ2）为透镜上的碰撞矢量。

以示意图中的“源1”为例来讨论光线路径方程。示意图中，Dd为观测者到透镜的距离，Dds为源到透镜的距离，Ds为观测者与源的距离。原则上Dd、Dds、Ds并不在直线z轴（测量角度所选的参考方向）上，但考虑到其横向距离远远小于纵向距离，因此忽略横向上的偏差而将纵向距离作为其空间距离。

示意图中各角度的意义分别为：β为引力透镜不存在时源的方向与z轴夹角；θ为引力透镜存在时，观测到的光线方向与z轴的夹角；α为光线的偏折角。值得一提的是，由于时空的弯曲，一般Ds≠Dd+ Dds。在小角度近似条件下（α、β、θ