[科普中国]-前进波

定义

亦称“行波”。在介质内向前传播的波。在深水中传播的前进波的水质点做圆周运动，在有限深度情况下，水质点的运动轨迹呈椭圆形。波峰处水质点的水平运动速度最大，其方向和波形传播的方向一致。波谷处水质点的水平运动速度也最大，其方向和波形传播方向相反。这样，在波峰的前方必然要发生水体堆积。同样，波峰的后方必然要发生水体流失，从而使波形向前传播。海浪多具有前进波性质。大洋潮波亦具有前进波性质。1

现象描述对于三维空间等深水中,无旋性自由表面周期性规则前进重力波传递在均匀流中的波流场,依质量守恒取—波长的流体质点的运动位移的波长平均高程,所得其标注参数恰为其在原静止水中的位置下,完全以Lagrange方式的参数控制式,解出此波流场至第三阶的全Lagrange形式解且得到检验验证;其中波流交互作用效应存在Lagrange流速势中,使得波流场中的压力不受均匀流的影响.而Euler形式解所无法描述的流场特性,包括大于前进波周期的流体质点的运动周期,与其受前进波引起的质量传输速度、它们间的关系,及流体质点对其运动周期平均的高程与成因等,都说明是随流体质点所在的高程向下做指数函数样递减;而流体质点的三维空间螺旋曲线式的运动轨迹与烟线,其随均匀流的流向流速而变化的情况,例如其在均匀流于前进波波向有同向的流速分量时,是受流体质点恰在波谷断面处时的流速大小而变的形式,与其在均匀流于前进波波向有反向的流速分量时,则受流体质点恰在波峰断面处时的流速大小而变的形式,有很大不同的倒反形式甚至以封闭曲线形式呈现.最后,说明波流场变成稳定性运动流场时的特性,并证实其在无流时退化成纯前进波的情况.2

产生机理非旋性自由表面周期性规则前进重力波传递在均匀流中的理论解析,与前进波波向同向与反向的均匀流两种特例情况进行试验测量,所得的波形曲线、流速分布、流体质点的运动轨迹与运动周期及其质量传输速率与Lagrange平均高程等特性,均以Lagrange方式所得的三阶解结果符合得很好.这证实本研究取定的标注流体质点的参数,正好为其在原静止水中的位置坐标值.同时亦证实波流场中由流体质点所构成的波形曲线,其波长皆同于(纯)前进波者,而其传播速度为(纯)前进波波速与均匀流流速之和是具Doppler效应的;而流体质点的运动周期与其运动周期平均高程,及其质量传输速率扣掉均匀流流速等,都与(纯)前进波的相符.另外,亦揭示出流体质点的运动轨迹,在前进波波向与均匀流同向中,当流体质点在波谷断面处时沿前进波波向的流速分量为反向、零与正向时,则其形状分别为朝波向前进的扁长辐状余摆线,在波谷断面处成尖点朝下的滚轮状线与短辐形余摆线;而在前进波波向与均匀流反向中,当流体质点的质量传输速率为沿前进波波向为正向与零时,则其形状分别为朝波向前进的缩短的扁长辐形余摆线与长轴在前进波波向上的椭圆形封闭曲线;而当流体质点的质量传输速率为反前进波波向,但质点在波峰断面处时沿前进波波向的流速分量分别为正向、零与反向时,则其形状分别为反波向前进的倒扁长辐形余摆线,在波峰断面处成尖点朝上的倒滚轮状线与倒短辐形余摆线.2

轨迹方程波形向前传播而水质点运动轨迹呈封闭或近似封闭的周期性振动的波浪。通常所指的波速即为波形向前传播的速度。微幅波理论的深水前进波水质点作圆周运动，轨迹圆圆心位置与静止时水质点的位置相吻合。水质点m的轨迹方程为：

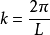
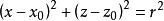x0，z0为水质点m在静止时的坐标;r为轨迹圆半径;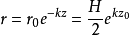;r0为自由表面轨迹圆半径;k为波数，;H为波高;L为波长。微幅波理论的浅水前进波水质点作椭圆运动，其轨迹方程为：

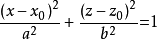a，b分别为轨迹椭圆的半长轴和半短轴。

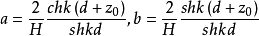
在前进波中初始位置在同一水平面上各水质点在波动时具有相同的轨迹圆或轨迹椭圆。在海洋、湖泊等宽敞水面上所发生的波浪常高达数米，其波陡一般约为 1/10～1/30 ，水质点的波动振幅是有限值的。这种前进波称为有限振幅前进波，也可分为深水和浅水两种情况，如余摆线波和椭圆余摆线波等。3

发生实例海坛海峡为南北狭长型海峡,海峡内潮波属于前进波.本文建立了平面二维浅水波数学方程,利用欧拉-拉格朗日差分方法得到数值解,模型采用随时间变化的动边界技术,成功地模拟了海坛海峡的前进波特征,并根据实测数据进行了验证.同时计算了同潮时线和等振幅线,不同时刻的潮流场和潮流平均流速分布.计算结果表明,北部湾口M2分潮高潮时间比南部湾口早约5~6m in,等振幅线范围约为2.12~2.15m.海峡内流速分布呈南北强、中间弱的特点,最大流速1m/s左右.