[科普中国]-全概率公式

定义

定理

若事件B1，B2，…构成一个完备事件组且都有正概率，则对任意一个事件A，有如下公式成立：

P(A)=P(AB1)+P(AB2)+...+P(ABn)=P(A|B1)P(B1) + P(A|B2)P(B2) + ... + P(A|Bn)P(Bn).

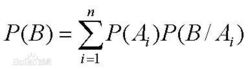
此公式即为全概率公式。

特别地，对于任意两随机事件A和B，有如下成立：

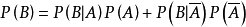
其中A和Ac为对立事件。

应用举例我们来看一个简单的例子：

例：高射炮向敌机发射三发炮弹，每弹击中与否相互独立且每发炮弹击中的概率均为0.3，又知敌机若中一弹，坠毁的概率为0.2，若中两弹，坠毁的概率为0.6，若中三弹，敌机必坠毁。求敌机坠毁的概率。

解：设事件B=“敌机坠毁”；Ai=“敌机中弹”；i=0,1,2,3

实际上我们从题目知道应该是A0,A1,A2,A3构成完备事件组，但是敌机坠毁只和A1,A2,A3有关，即
，则我们可用如下公式：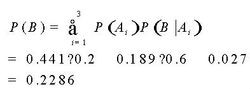

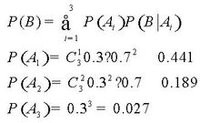
全概率公式和Bayes公式概率论的一个重要内容是研究怎样从一些较简单事件概率的计算来推算较复杂事件的概率，全概率公式和Bayes公式正好起到了这样的作用。对一个较复杂的事件A，如果能找到一伴随A发生的完备事件组B1、B2```，而计算各个B的概率与条件概率P(A/Bi)相对又要容易些，这时为了计算与事件A有关的概率，可能需要使用全概率公式和Bayes公式。