[科普中国]-同态处理

一种特定的数字信号处理方法.利用同态系统把一类输入信号变换为另一类信号输出的过程称为同态信号处理。例如，对输入为乘法组合的信号或者卷积组合的信号，通过同态系统就可以得到另一种组合的输出信号。同态系统可以把非线性组合的信号，通过变换用线性系统对它进行处理。1

简介用同态系统进行信号处理。同态系统是服从广义叠加原理、在代数运算上可用输入和输出的矢量空间之间的线性变换来表征的非线性系统。对于卷积性信号，其频谱是相互叠加在一起的。不能通过简单的滤波器将其分开，需要对信号进行同态处理。

同态处理又称同态信号处理。在信号处理中，常需从带有噪声的信号中提取原始信号。一般用滤波处理方法滤除或削弱噪声干扰以及其他不需要的信号。对于叠加性组合信号，可用线性滤波器将它们分离开。对于实用中常见的非叠加性 组合信号（如乘积性信号和褶积性信号），靠线性滤波器分离或处理这些信号分量往往是无效的，这时应采用非线性滤波，即要用同态滤波处理系统进行信号处理。在输入输出运算相同的情况下，同态系统可分为相乘信号的同态滤波处理和褶积信号的同态滤波处理两种。

在许多实际问题中，信号为两个或多个分量的乘积（如在有衰落的传输信道中，衰落效应可看作一个缓变分量和传输信号相乘）。对这类相乘信号，如用线性系统来分离信号各成分或单独地改善某一信号成分往往是无效的。但利用相乘信号的同态滤波处理，就可以取得较好的滤波效果。在多径或混响环境中进行通信、定位或记录，产生失真的效果可以看成是干扰与所需信号的褶积，对这类信号可用褶积信号的同态滤波处理。在语音、图像、雷达、声呐、地震勘探以及生物医学工程等领域中，同态信号处理获得广泛的应用。

算法步骤比如语音信号可以视为声门激励信号与声道冲激响应的卷积。同态语音信号分析的目的就是将激励源与声道冲激响应分开来分别进行研究，尽量获得准确的激励源与声道冲激响应的估计，这也成为解卷算法。

解卷算法分为两大类：

一类是为线性系统建立模型，然后按照某种准则对模型进行参数估计，即“参数解卷”，比如线性预测分析技术。

二类是无须建立模型。称之为”非参数解卷“。同态处理就是其中的一种。它可以实现将激励源与声道冲激响应的卷积关系变换为求和关系，通过滤波进一步分离两种信号。

假设输入信号为：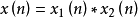

它采用三步数学运算：

1、Z变换：时域中的将卷积运算转换为频域中的乘积运算。

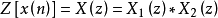
2、对数运算：将乘积运算转换为加性运算。

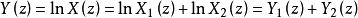
3、逆Z变换：将频域转换到时域中来。

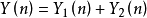
其中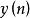是一个时间序列的Z变换的对数所对应的时间序列，称为复倒谱。

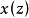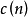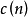如果忽略的相位信息，只考虑幅度信息，那么立刻得到倒谱的定义：定义为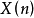 Z变换后的幅度的对数的逆Z变换，即

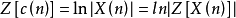
同态系统原理利用同态系统进行图像增强处理是把频率过滤和灰度变换结合起来的一种处理方法。它是把图像的照明反射模型作为频域处理的基础，利用压缩亮度范围和增强对比度来改善图像的一种处理技术。2

由于子系统是“确定的一种特征系统，因此称为对运算的特征系统。同样是对运算的特征系统。显然，具有相同运算规则的第一子系统和第三子系统的所有同态系统，只是其线性系统部分有所不同。换言之，特征系统确定之后，剩下的就是线性滤波问题了。

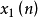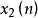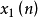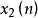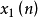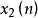因此，为了分离 和 ，必须用一个线性滤波器L来完全分离 和 。理想的分离取决于运算法则“囗”以及输入信号分量 和 的性质。

同态滤波处理系统 在输入和输出运算相同的情况下，同态系统可分为相乘信号的同态滤波处理和褶积信号的同态滤波处理两种。

应用在许多实际问题中，信号为两个或多个分量的乘积。例如，在有衰落的传输信道中，衰落效应可以看作是一个缓变分量和传输信号相乘。又如，调幅信号可表示为载频信号与包络函数的乘积，在接收机内需要分离载波和包络。在这一类相乘信号中，用线性系统来分离信号各成分或单独地改善某一信号成分往往是无效的。但利用相乘信号的同态滤波处理，就可以取得较好的滤波效果。

褶积信号的同态滤波处理 在多径或混响环境中进行通信、定位或记录，产生失真的效果可以看成是干扰与所需信号的褶积。在语音信号处理中，经常要分离激励源与声道冲激响应，至少在一段短时间内可以认为语音波形是由两者的褶积构成的。地震记录数据是地震子波与含有岩层结构信息的反射系数序列的褶积组合。离散褶积组合信号可以表示为 。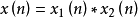

Z变换运算也可以看作是一个系统，它的输入运算为褶积，输出运算是乘法的同态变换。因此，利用Z变换就能把褶积组合变换成乘法组合，从而可以利用上述乘法同态滤波系统来处理。但是，通常函数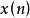 是个复数，故不得不采用复对数运算。

本词条内容贡献者为:

何星 - 副教授 - 上海交通大学