在数学中,范畴(category),是一种包含了对象及对象之间箭头的代数结构。范畴具有两个基本性质:一是对象之间的箭头可以复合,且复合是满足结合律的;二是每个对象到自己有一个单位箭头。一个简单的范畴例子是由集合构成对象,集合间的映射看做箭头。一般来说,对象和箭头可以是抽象的任何类型,范畴的概念提供了一个基本而抽象的方式去研究数学中的对象及其关系的方法。
定义一个范畴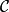 ,是由以下要素组成1:
,是由以下要素组成1:
(1) 一些对象(通常用大写字母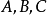 等表示)构成的一个类
等表示)构成的一个类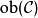 ;
;
(2)由所有的集合 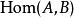 构成的族,这里
构成的族,这里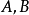 取遍
取遍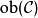 中的所有对象。
中的所有对象。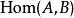 中的元素
中的元素 称为从
称为从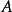 到
到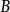 的态射(morphism),记为
的态射(morphism),记为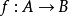 ;
;
(3)对于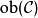 中任意三个对象
中任意三个对象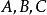 ,存在二元算子
,存在二元算子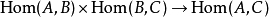 ,成为态射的复合,记
,成为态射的复合,记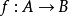 和
和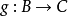 的复合为
的复合为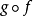 或
或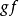 ,使得下面的公理成立:
,使得下面的公理成立:
(i)(结合律)如果有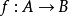 ,
,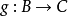 和
和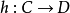 ,则
,则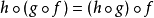 ;
;
(ii)(单位元)对每个对象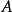 ,有单位态射
,有单位态射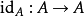 ,使得对任意的
,使得对任意的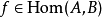 ,有
,有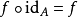 ,且对任意的
,且对任意的 ,有
,有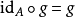 。
。
范畴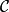 中的一个态射
中的一个态射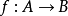 被称为同构,如果存在一个态射
被称为同构,如果存在一个态射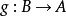 ,使得
,使得 ,
,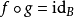 。这时,我们也称对象
。这时,我们也称对象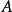 和
和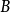 是同构的。一个广群是一个范畴,满足其中任意态射都是同构。
是同构的。一个广群是一个范畴,满足其中任意态射都是同构。
小范畴一个范畴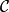 被成为小范畴(small category),如果它的对象类
被成为小范畴(small category),如果它的对象类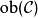 是一个集合。一个范畴
是一个集合。一个范畴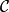 被称为基本小(essentially small),如果它的对象的同构类是一个集合。显然小范畴总是基本小的。
被称为基本小(essentially small),如果它的对象的同构类是一个集合。显然小范畴总是基本小的。
例子每一范畴都可由其物件、态射和态射复合来表示。
1.所有集合的范畴Set,其态射为集合间的函数,而态射复合则为一般的函数复合。(下列皆为具体范畴的例子,即在Set上加入一些结构,且要求态射为对应于此附加结构的函数,态射复合则为简单的一般函数复合。)
1) 所有预序关系的范畴,其态射为单调函数;
2) 所有原群的范畴,其态射为原群间的同态。
3) 所有群的范畴,其态射为群间的群同态;
4) 所有阿贝尔群的范畴,其态射为群间的群同态;
5) 所有环的范畴,其态射为环同态。
6)所有于体K(维持固定)上的向量空间的范畴,其态射为线性映射;
7) 所有拓朴空间的范畴,其态射为连续函数;
8) 所有度量空间的范畴,其态射为度量映射;
9) 所有一致空间的范畴,其态射为一致连续函数;
10) 所有光滑流形的范畴,其态射为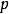 次连续可微映射;
次连续可微映射;
11) 所有小范畴的范畴,其态射为函子;
12) 所有集合的范畴,其态射为关系。
2. 任意一个偏序集 构成一个范畴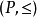 ,对象是
,对象是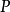 中的元素,存在一个从
中的元素,存在一个从 到
到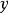 的态射当且仅当
的态射当且仅当 。恒等态射和态射的复合由偏序的自反性和传递性给出。这是一个小范畴。
。恒等态射和态射的复合由偏序的自反性和传递性给出。这是一个小范畴。
3. 任一幺半群都会形成一个具单一个物件 的小范畴(此处的x是任一个固定的集合)。从
的小范畴(此处的x是任一个固定的集合)。从 至
至 的态射恰好是幺半群的元素,且其态射复合由幺半群的运算所给定。幺半群令态射绝不可能为函数,唯一从单元素集合x至x的函数为当然函数。可视范畴为广义化了的幺半群;一些和幺半群有关的定义和定理也可能可以义广化成范畴的定义和定理。
的态射恰好是幺半群的元素,且其态射复合由幺半群的运算所给定。幺半群令态射绝不可能为函数,唯一从单元素集合x至x的函数为当然函数。可视范畴为广义化了的幺半群;一些和幺半群有关的定义和定理也可能可以义广化成范畴的定义和定理。
4. 任一有向图都会产生一个小范畴:其物件为图的顶点,态射为图中的路径,而态射复合则为路径的串接。这被称之为由图产生出的“自由范畴”。
5.若I是一个集合,“在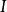 上的具体范畴”会是个小范畴,其物件为的元素,而态射则只有单位态射。当然,其态射复合的公理是必然满足的。
上的具体范畴”会是个小范畴,其物件为的元素,而态射则只有单位态射。当然,其态射复合的公理是必然满足的。
6.任一范畴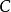 皆可以另一种方式被视为是一个新的范畴:其物件和原范畴的一样,但态射则和原范畴相反。这被称之为对偶范畴,标记为
皆可以另一种方式被视为是一个新的范畴:其物件和原范畴的一样,但态射则和原范畴相反。这被称之为对偶范畴,标记为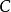 。
。
7.若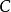 和
和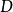 为范畴,可形成一“积范畴”
为范畴,可形成一“积范畴”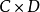 :其物件为由
:其物件为由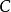 和
和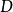 内的物件所组成的对,且态射亦为由
内的物件所组成的对,且态射亦为由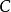 和
和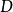 内的态射所组成的对。这些对的态射复合是由各元素各自复合。
内的态射所组成的对。这些对的态射复合是由各元素各自复合。
范畴类型1.在许多范畴中,例如阿贝尔群范畴或向量空间范畴,态射集合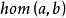 不仅是集合,而且还是阿贝尔群,并且态射的复合与这些阿贝尔群之间的群结构兼容,即复合映射是双线性的。这种范畴称为预可加范畴。如果在此基础上这个范畴还带有所有有限积和上积,那么我们称之为可加范畴。如果更进一步地,所有态射都有核和上核,并且每个满态射都是上核而每个单态射都是核,那么我们称之为阿贝尔范畴。阿贝尔范畴的典型例子是阿贝尔群的范畴。
不仅是集合,而且还是阿贝尔群,并且态射的复合与这些阿贝尔群之间的群结构兼容,即复合映射是双线性的。这种范畴称为预可加范畴。如果在此基础上这个范畴还带有所有有限积和上积,那么我们称之为可加范畴。如果更进一步地,所有态射都有核和上核,并且每个满态射都是上核而每个单态射都是核,那么我们称之为阿贝尔范畴。阿贝尔范畴的典型例子是阿贝尔群的范畴。
2.范畴是完备的当其拥有所有极限。集合、阿贝尔群、拓扑空间的范畴都是完备的。
3.范畴是笛卡尔闭的当其拥有所有有限直积、且有限积上的态射总是可由任一因子上的态射确定。笛卡尔闭范畴包括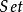 和
和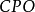 ,即完全偏序和斯科特连续函数组成的范畴。
,即完全偏序和斯科特连续函数组成的范畴。
4.拓扑斯是一种特定的笛卡尔闭范畴;所有数学内容都可以用拓扑斯的语言形式化(正如所有经典数学都可以用集合范畴的语言形式化一般)。拓扑斯也可用于表示逻辑理论2。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国