如果一个矩阵的任何子方阵的行列式等于1,-1或0,则称这个矩阵是全单位模矩阵。把m阶单位矩阵用Im表示。显然,Im是全单位模矩阵1。
定义如果一个矩阵的任何方阵的行列式等于1,-1或0,则称该矩阵为全单位模矩阵(total unimodular matrix)。
不难知道,全单位模矩阵的一个明显的必要条件是它的元素为1,-1或0,下面的定理给出了全单位模矩阵的一个充分条件。
定理1 设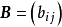 ,且对一切
,且对一切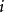 和
和 或0,如果下面两个条件都满足,则
或0,如果下面两个条件都满足,则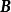 是全单位模矩阵。
是全单位模矩阵。
(1)B的每一列最多有两个非零元素;
(2) B的行可分划成两个子集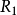 和
和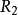 ,使得对于同一列中两个非零元素,当这两个非零元素符号相同时,对应的两行在不同的行子集中;当符号不同时,对应的两行在同一行子集中。
,使得对于同一列中两个非零元素,当这两个非零元素符号相同时,对应的两行在不同的行子集中;当符号不同时,对应的两行在同一行子集中。
证明: 用归纳法证明。只需证明B的任何一个子方阵**B'的行列式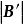 =1,-1或0,设B'**是n阶方阵,对n进行归纳.若n=1时,则显然成立。
=1,-1或0,设B'**是n阶方阵,对n进行归纳.若n=1时,则显然成立。
由于B满足(1)和(2),因此B的任何子矩阵也满足这两个条件,假设B的任何k阶子方阵的行列式等于1,-1或0,任取B的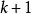 阶子方阵B',它也满足条件(1)和(2),如果**B'的某一列恰有一个非0元素,记该元素在B'中的余子式为b,则
阶子方阵B',它也满足条件(1)和(2),如果**B'的某一列恰有一个非0元素,记该元素在B'中的余子式为b,则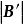 =±b,由归纳假设,b=1,-1或0,从而
=±b,由归纳假设,b=1,-1或0,从而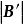 =1,-1或0;如果B'的每一列恰有两个非零元素,则对B'**中任何列
=1,-1或0;如果B'的每一列恰有两个非零元素,则对B'**中任何列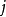 ,有
,有
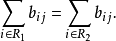 把**B'的第
把**B'的第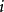 行记为
行记为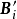 ,则
,则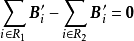 ,即B'**的所有行向量是线性相关的,故
,即B'**的所有行向量是线性相关的,故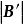 =02。
=02。
相关性质定理2非空无环有向图的关联矩阵是全单位模的。
顺便指出:图的关联矩阵不一定是全单位模矩阵,例如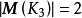 。
。
定理3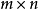 全单位模矩阵A有下列性质:
全单位模矩阵A有下列性质:
(1)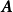 的任何子矩阵是全单位模矩阵。
的任何子矩阵是全单位模矩阵。
(2)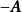 和
和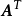 是全单位模矩阵。
是全单位模矩阵。
(3) 把A的两行互换得到的矩阵是全单位模矩阵。
(4) 把A的两列互换得到的矩阵是全单位模矩阵。
(5)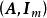 和
和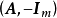 是全单位模矩阵。
是全单位模矩阵。
(6)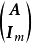 和
和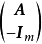 是全单位模矩阵。
是全单位模矩阵。
(7) 设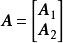 ,则
,则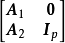 和
和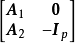 是全单位模矩阵。
是全单位模矩阵。
(8) 设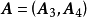 ,则
,则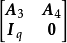 和
和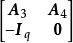 是全单位模矩阵。
是全单位模矩阵。
**证明:**性质(1)、(2)、(3)、(4) 是显然的。
下证(5)。
设B是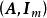 的任一非奇异子矩阵,若B是A或
的任一非奇异子矩阵,若B是A或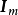 的子矩阵,则B的行列式的绝对值|det B|=1;否则,设
的子矩阵,则B的行列式的绝对值|det B|=1;否则,设
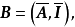 这里
这里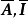 分别是
分别是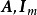 的子矩阵。互换B的某些行可得
的子矩阵。互换B的某些行可得
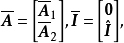 其中
其中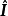 为单位矩阵。记
为单位矩阵。记
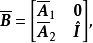 注意到
注意到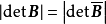 ,并且
,并且
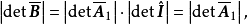 由于A是全单位模矩阵,故
由于A是全单位模矩阵,故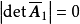 或1,又因B是非奇异矩阵,所以|detB|=1,这就证明了
或1,又因B是非奇异矩阵,所以|detB|=1,这就证明了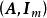 是全单位模矩阵。同理可证:
是全单位模矩阵。同理可证: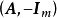 也是全单位模矩阵。
也是全单位模矩阵。
由(2)和(5)知,(6)成立。
根据证明(5)的类似推理,不难证明(7)。
(8)可以由(2)和(7)得到。
关于整数线性规划问题网络最优化的许多问题常常可以用一个整数线性规划模型来描述。整数线性规划是指要求变量取整数值的线性规划1。
考虑整数线性规划问题
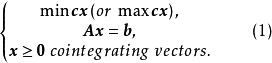 这里,“
这里,“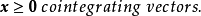 ”是指
”是指 的每个分量都是非负整数。所有元素均是整数的矩阵称为整数矩阵。所有分量都是整数的向量称为整向量。我们假定(1)式中的A是整数矩阵,b是整向量。
的每个分量都是非负整数。所有元素均是整数的矩阵称为整数矩阵。所有分量都是整数的向量称为整向量。我们假定(1)式中的A是整数矩阵,b是整向量。
在整数线性规划问题(1)式中去掉整数约束就得到线性规划问题
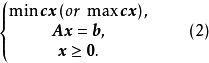 如果(2)式的可行解
如果(2)式的可行解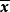 是整向量,则称
是整向量,则称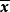 为(2)式的整数解。如果(2)式的最优解
为(2)式的整数解。如果(2)式的最优解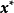 是整数解。则称
是整数解。则称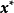 是(2)式的最优整数解。因此,整数线性规划问题(1)式的求解可以化为求线性规划问题(2)式的最优整数解。
是(2)式的最优整数解。因此,整数线性规划问题(1)式的求解可以化为求线性规划问题(2)式的最优整数解。
定理4 设A为行满秩整数矩阵,则下面三个条件等价:
(i) A的任意基矩阵B的行列式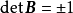 ;
;
(ii) 对于任意整向量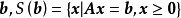 的极点的每个分量都是整数。
的极点的每个分量都是整数。
(iii) A的任何基矩阵B的逆矩阵B-1都是整数矩阵。
定理5 设A是全单位模矩阵,如果线性规划问题(2)式有最优解,则(2)式必有最优整数解1。
由定理5知,若A是全单位模矩阵,则整数线性规划问题(1)式中的整数约束可以去掉而化为线性规划问题(2)式来求解。
考虑整数线性规划问题问题
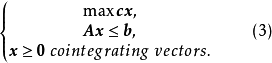 这里A是整数矩阵,b是整向量。它对应的线性规划问题为
这里A是整数矩阵,b是整向量。它对应的线性规划问题为
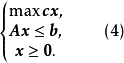 因为
因为 等价于
等价于
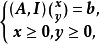 其中
其中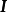 是单位矩阵。并且由定理3中的(5)和(1)知:A为全单位模矩阵当且仅当
是单位矩阵。并且由定理3中的(5)和(1)知:A为全单位模矩阵当且仅当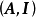 为全单位模矩阵。
为全单位模矩阵。
定理6 设A是全单位模矩阵,则整数线性规划问题(3)式中的整数约束可以去掉而化为线性规划问题(4)式。
定理5和定理6是整数线性规划中两个重要的结论,它们表明:在一定条件下,整数线性规划可以化为线性规划来解。这就大大简化了整数线性规划的求解1。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国