[科普中国]-信源编码

信源编码是一种以提高通信有效性为目的而对信源符号进行的变换，或者说为了减少或消除信源利余度而进行的信源符号变换。具体说，就是针对信源输出符号序列的统计特性来寻找某种方法，把信源输出符号序列变换为最短的码字序列，使后者的各码元所载荷的平均信息量最大，同时又能保证无失真地恢复原来的符号序列。1

编码结果对输入信息进行编码，优化信息和压缩信息并且打成符合标准的数据包。

作用信源编码的作用之一是，即通常所说的数据压缩；作用之二是将信源的模拟信号转化成数字信号，以实现模拟信号的数字化传输。

方式最原始的信源编码就是莫尔斯电码，另外还有ASCII码和电报码都是信源编码。但现代通信应用中常见的信源编码方式有：Huffman编码、算术编码、L-Z编码，这三种都是无损编码，另外还有一些有损的编码方式。信源编码的目标就是使信源减少冗余，更加有效、经济地传输，最常见的应用形式就是压缩。

另外，在数字电视领域，信源编码包括 通用的MPEG—2编码和H.264（MPEG—Part10 AVC）编码等。

相应地，信道编码是为了对抗信道中的噪音和衰减，通过增加冗余，如校验码等，来提高抗干扰能力以及纠错能力。

定理不同类型的信源，是否存在有每种信源的最佳的信源编码，这通常是用信源编码定理来表示。最简单、最有实用指导意义的信源编码定理是离散、无记忆型信源的二进制变长编码的编码定理。它证明，一定存在一种无失真编码，当把N个符号进行编码时，平均每个符号所需二进码的码长满足。

其中H（U）是信源的符号熵（比特），这就是说，最佳的信源编码应是与信源信息熵H（U）统计匹配的编码，代码长度可接近符号熵。这一结论不仅表明最佳编码存在，而且还给出具体构造码的方法，即按概率特性编成不等长度码。对不同类型信源，如离散或连续、无或有记忆、平稳或非平稳、无或限定失真等，可以构成不同的组合信源，它们都存在各自的信源编码定理。但它们中绝大部分仅是属于理论上的存在性定理，这给具体寻找和实现不同类型信源的信源编码，带来了相当的难度。

分类信源编码根据信源的性质进行分类，则有信源统计特性已知或未知、无失真或限定失真、无记忆或有记忆信源的编码；按编码方法进行分类可分为分组码或非分组码、等长码或变长码等。然而最常见的是讨论统计特性已知条件下，离散、平稳、无失真信源的编码，消除这类信源剩余度的主要方法有统计匹配编码和解除相关性编码。比如仙农码、费诺码、赫夫曼码，它们属于不等长度分组码，算术编码属于非分组码；预测编码和变换编码是以解除相关性为主的编码。对限定失真的信源编码则是以信息率失真R（D）函数为基础，最典型的是矢量量化编码。对统计特性未知的信源编码称为通用编码。

应用以简单的数据压缩为例即可说明信源编码的应用。若有一离散、无失真、无记忆信源，它含有五种符号U0～U4及其对应概率Pi，对它进行两种编码：等长码和最佳赫夫曼码（见表1）。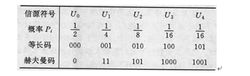

其中，等长码的平均码长：=3，即三位码。若采用赫夫曼编码，平均码长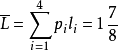，即不足两位码。这就是说，数据压缩了以上。

通信系统模型[信源]->[信源编码]->[信道编码]->[信道传输+噪声]->[信道解码]->[信源解码]->[信宿]

一般信息论的书上都会有信源编码和信道编码的具体讲解，包括具体的编码方法。

专业表述既然信源编码的基本目的是提高码字序列中码元的平均信息量，那么，一切旨在减少剩余度而对信源输出符号序列所施行的变换或处理，都可以在这种意义下归入信源编码的范畴，例如过滤、预测、域变换和数据压缩等。当然，这些都是广义的信源编码。

一般来说，减少信源输出符号序列中的剩余度、提高符号平均信息量的基本途径有两个：①使序列中的各个符号尽可能地互相独立；②使序列中各个符号的出现概率尽可能地相等。前者称为解除相关性，后者称为概率均匀化。

信源编码的一般问题可以表述如下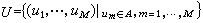：若某信源的输出为长度等于M的符号序列集合 式中符号A为信源符号表，它包含着K个不同的符号，A={ɑk|k=1,…,K}，这个信源至多可以输出KM个不同的符号序列。记‖U‖=KM。所谓对这个信源的输出进行编码，就是用一个新的符号表B的符号序列集合V来表示信源输出的符号序列集合U。若V的各个序列的长度等于 N，即 式中新的符号表B共含L个符号，B={bl|l=1,…,L}。它总共可以编出LN个不同的码字。类似地,记‖V‖=LN。为了使信源的每个输出符号序列都能分配到一个独特的码字与之对应，至少应满足关系 ‖V‖=LN≥‖U‖=KM

或者 N/M≥logK/logL

假若编码符号表B的符号数L与信源符号表A的符号数K相等，则编码后的码字序列的长度N必须大于或等于信源输出符号序列的长度M；反之，若有N=M，则必须有L≥K。只有满足这些条件，才能保证无差错地还原出原来的信源输出符号序列(称为码字的唯一可译性)。可是，在这些条件下，码字序列的每个码元所载荷的平均信息量不但不能高于，反而会低于信源输出序列的每个符号所载荷的平均信息量。这与编码的基本目标是直接相矛盾的。下面的几个编码定理，提供了解决这个矛盾的方法。它们既能改善信息载荷效率，又能保证码字唯一可译。

离散无记忆信源的定长编码定理

对于任意给定的ε>0，只要满足条件 N/M≥(H(U)+ε)/logL

那么，当M足够大时，上述编码几乎没有失真;反之,若这个条件不满足，就不可能实现无失真的编码。式中H(U)是信源输出序列的符号熵。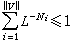通常，信源的符号熵H(U)