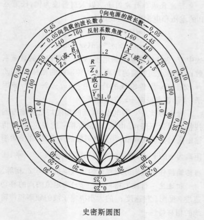
史密夫图表(Smith chart,又称史密斯圆图)是在反射系散平面上标绘有归一化输入阻抗(或导纳)等值圆族的计算图。是一款用于电机与电子工程学的图表,主要用于传输线的阻抗匹配上。
简介史密夫图表(Smith chart,又称史密斯圆图)是在反射系散平面上标绘有归一化输入阻抗(或导纳)等值圆族的计算图。是一款用于电机与电子工程学的图表,主要用于传输线的阻抗匹配上。该图由三个圆系构成,用以在传输线和某些波导问题中利用图解法求解,以避免繁琐的运算。一条传输线(transmission line)的电阻抗力(impedance)会随其长度而改变,要设计一套匹配(matching)的线路,需要通过不少繁复的计算程序,史密夫图表的特点便是省略一些计算程序。1
特点该图表是由菲利普·史密斯(Phillip Smith)于1939年发明的,当时他在美国的RCA公司工作。一年後,一位名为Kurakawa的日本工程师也声称发明了这种图表。史密斯曾说过,“在我能够使用计算尺的时候,我对以图表方式来表达数学上的关联很有兴趣”。
由于采用了归一化措施,所以适用于任何特性阻抗和任意波长。精度则取决于圆图的刻度。
阻抗圆图由等电阻 (Ri)圆系、等电抗Xi圆系和|Γ|圆系构成,见图1。其中Ri和Xi分别是归一化输入阻抗 的实部和虚部,
的实部和虚部,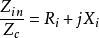 。
。
|Γ|是反射系数Γ的模。为避免图上线条太多,|Γ|圆系一般不画出。
史密斯圆图的用途是多方面的:根据归一化负载阻抗ZL/ZC,可求得反射系数Γ,在Γ=|Γ|∠θ已知的情况下可得到ZL/ZC。当ZL/ZC、归一化长度(1/λ)巳知时可查出Zin/ZC。在Zin/ZC和归一化长度已知时可得到ZL/ZC,而当Zin/ZC和ZL/ZC已知时可求出这段传输线的长度。在驻波比及第一个电压最小点到传输线终端的距离已知时,利用此图可以查出的ZL/ZC数值。
导纳圆圈由等电导 (Gi)圆系、等电纳 (Bi)圆系和|Γ|圆系构成。其中,Gi及Bi分别为归一化输入导纳Yin/YC的实部和虚部。
导纳圆图与阻抗圆图的形式一样,只是阻抗圆图中的Ri、Xi由Gi、Bi替代。常用于并联电路的计算。
算式史密斯图表的基本在于以下的算式

当中的Γ代表其线路的反射系数(reflection coefficient),即S参数(S-parameter)里的S11,ZL是归一负载值,即ZL / Z0。当中,ZL是线路本身的负载值,Z0是传输线的特征阻抗(本征阻抗)值,通常会使用50Ω。
图表中的圆形线代表电阻抗力的实数值,即电阻值,中间的横线与向上和向下散出的线则代表电阻抗力的虚数值,即由电容或电感在高频下所产生的阻力,当中向上的是正数,向下的是负数。图表最中间的点(1+j0)代表一个已匹配(matched)的电阻数值(ZL),同时其反射系数的值会是零。图表的边缘代表其反射系数的长度是1,即100%反射。在图边的数字代表反射系数的角度(0-180度)和波长(由零至半个波长)。
有一些图表是以导纳值(admittance)来表示,把上述的阻抗值版本旋转180度即可。
自从有了计算机后,此种图表的使用率随之而下,但仍常用来表示特定的资料。对于就读电磁学及微波电子学的学生来说,在解决课本问题仍然很实用,因此史密夫图表仍是重要的教学用具。
在学术论文里,量度仪器的结果也常会以史密夫图表来表示。2
圆图意义基本意义1.阻抗圆的上半圆内,x>0,其电抗为感抗,下半圆内,x




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国