[科普中国]-布拉格方程

布拉格方程：对于X射线衍射，当光程差等于波长的整数倍时，晶面的散射线将加强，此时满足的条件为2dsinθ=nλ，其中，d为晶面间距，θ为入射线，反射线与反射晶面之间的夹角，λ为波长，n为反射级数，布拉格方程是X射线在晶体产生衍射时的必要条件而非充分条件。有些情况下晶体虽然满足布拉格方程，但不一定出现衍射，即所谓系统消光。

定义布拉格方程是给出晶体X射线衍射条件的方程。1

2dsinθ=nλ，n=1,2…

其中，d为晶面间距，θ为入射X射线与相应晶面的夹角，λ为X射线的波长，n为衍射级数，其含义是：只有照射到相邻两晶面的光程差是X射线波长的n倍时才产生衍射。上式表明，当晶面与X射线之间满足上述几何关系时，X射线的衍射强度将相互加强。

推导设一单色波（任何种类），进入一组对齐的平面晶格点，其平面间距为d，入射角为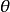，如右图所示。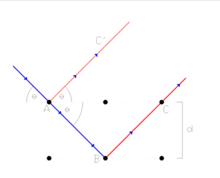波被晶格点A反射后会沿AC'行进，而没有被反射的波则沿AB继续行进，被晶格点B反射后路径为BC。AC'与BC间存在路径差，表达式为

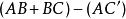
只有在路径差等于波长的整数倍时，这两股分开的波，在到达某一点时，会是同相位的，才会因此产生相长干涉，故相长干涉的产生条件为

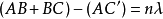， （需要为C'下定义）

其中 n与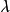的定义同上。

从上图可见，

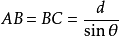且 ，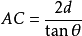

由此可得，

。

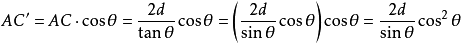组合上述各式，得

，

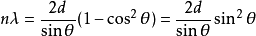简化后可得：

，

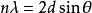即布拉格方程。

布拉格可见光散射胶体晶体为一种非常有序的粒子阵列，可以在大范围内形成（长度从几微米到几毫米不等），而且可被看作原子及分子晶体的类比。球状粒子的周期性阵列，会形成出相似的空隙阵列，而这种阵列可被用作可见光的衍射光栅，尤其是当空隙与入射波长为同一数量级的时候。

因此，科学家们在很多年前就发现了，由于相斥库仑相互作用的关系，水溶液中的带电荷高分子，会表现出大范围的类晶体相互关联，当中粒子间距一般会比粒子直径要大得多。在自然的所有这种例子中，都可到看到一样的漂亮构造色（或晃动的色彩），这都可以归功于可见光波的相长干涉，而此时光波会满足布拉格条件，跟结晶固体的X射线衍射类似。

应用该方程是晶体衍射的理论基础。是衍射分析中最重要的基础公式，它简单明确地阐明衍射的基本关系，应用非常广泛。归结起来，从实验上可有两方面的应用：

一、用已知波长的X射线去照射未知结构的晶体，通过衍射角的测量求得晶体中各晶面的间距d，从而揭示晶体的结构，这就是结构分析（衍射分析）；

二、用已知晶面间距的晶体来反射从样品发射出来的X射线，通过衍射角的测量求得X射线的波长，这就是X射线光谱学。该法除可进行光谱结构的研究外，从X射线波长尚可确定试样的组成元素。电子探针就是按照这一原理设计的。2

另见晶格

衍射

分散式布拉格反射器

光纤布拉格光栅

亨德森极限

衍射的动力学理论

劳厄方程

粉末衍射

结构因子

威廉·劳伦斯·布拉格

X射线晶体学

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所