[科普中国]-费米气体模型

提出

费米 气体模型2是E.Fermi在1932年提出的最原始的独立粒子模型，他把核子（中子和质子）看成是几乎没有相互作用的气体分子，把原子核简化为一个球体，核子在其中运动，遵守 Pauli 不相容原理。

把原子核视同一团气体，视同气体分子的核子（费米子）在半径为R的核内彼此无相互作用地自由运动，因而可视为在无限深势阱中运动的模型。由此计算核能级并给出激发态的一些有用信息。费米气体模型的成功之处，是揭示了原子核中核子在一定条件下近乎独立的行为，在它的基础上今已发展成为壳层模型。

原子核结构模型1. 原子核是一个有限量子多体系统3。

2. 由于核子间复杂的相互作用（QCD 在核子层次上的非微扰效应）以及多体耦合效应，理论上对原子核的描述,目前还没有一个统一的理论模型。针对不同质量区原子核通常采用不同原子核结构模型来描述。

3. 对原子核的集体运动则常采用唯象的模型或半经典的近似处理。

半唯象的理论在一定的实验事实的基础上，对原子核作某种模型假设，用来解释原子核的某些性质。

微观理论对核子间的作用力做一定假设后，代入多体哈密顿量中借用某种近似方法进行求解。

ab initio 方法采用拟合核子散射数据得到两 体和三体力, 来直接计算其基态和激发态性质。

费米气体模型介绍费米气体模型把核子看作几乎没有相互作用的气体分子，由于核子是费米子，原子核就可以是为费米气体。每个核子受其余核子形成的总的势场作用，就好象都是在一个势阱中。由于核子是费米子，原子核就可看成是费米气体，所以，对核内核子运动起约束作用的主要因素就是 Pauli 不相容原理4。

由于中子和质子有电荷差异，它们的核势阱的形状和深度都各不相同。

Pauli原理不能有两个全同的Fermi子处于同一个单粒子态5.

由于中子和质子有电荷差异，因此它们的核势阱的形式和深度不相同，质子阱的底就比中子阱高出库仑能Ec。

势阱内有一定的分立能级，当原子核处于 基态时，核子都处于它们可能处的最低能态。

每一个能级上可以有两个中子（或质子），一个自旋向上，一个自旋向下。

基态时核子可以处的最高能级的位置称之为费米能级EF。

费米能级三维势阱与一维情况相比，能量简并度大为提高。 对于基态，（n1,n2,n3）=(1,1,1),即只有一个基态。 第一激发态却有三个，（2，1，1），（1，2，1），（1，1，2），它们都有相同的能量。随着能量的增加，简并度也随之增高。

d为势阱宽度

费米半径公式为：

能态数可表示为

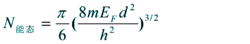
能态数为1/8球体积

中子数可表示为

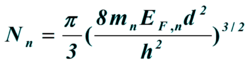
核体积：

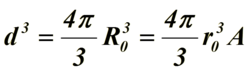
费米能量可表示为

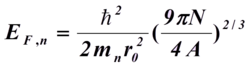
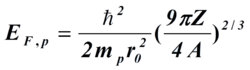
核子的最大动量可以表示为

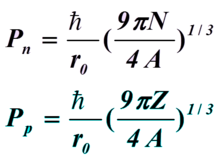
核子的平均动能可表示为

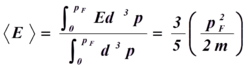
原子核的平均动能可以表示为

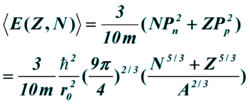
对称能设 Z - N = d 则

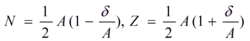
原子核平均动能

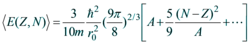
优缺点气体模型成功之处，在于它可以证明质子数和中子数相等的原子核最稳定。这一结论与事实相符。再有，用气体模型计算出的核势阱深度与其它方法得到的结果接近。不过这一模型没有考虑核子之间的强相互作用，过于简单，难以解释后来发现的许多新事实3。

相关模型壳层模型原子核内的核子在其余的核子产生的平均势场作用下独立地运动着，核子所受到的作用势只与它自己的坐标有关。求解这一平均势场下的薛定谔方程，可以得到这一核子的能级及相应的波函数。核子的能级往往是简并的，有些能级虽然不是简并的，但它们有相近的能量。这些具有相等或相近能量的状态构成一个壳层。一个壳层与下一个壳层有较大的能量差别核子按泡利不相容原理逐一填充这些状态,填满一个壳层后，就开始填充能量较高的另一个壳层，这时原子核的能量显得突然增加。所以，恰巧填满一个壳层的那些核显得特别稳定6。

壳层模型相当成功地描述了幻数，很好地解释了原子核基态的自旋和宇称（见核性质），解释了长寿命同质异能态的分布随核子数变化的规律，给出了核磁矩变化的趋势等等。

集体模型实验表明，原子核的运动形式，除了独立粒子运动以外，还有振动和转动等集体运动的形式。1952年丹麦物理学家A.玻尔和B.R.莫特森提出了一种新的核模型──集体模型（或叫做综合模型）。

集体模型认为，原子核中的核子在平均场中独立地运动并形成壳层结构,而原子核又可以发生形变,并产生转动和振动等集体运动。这两种集体运动的引入是集体模型对壳层模型的重要发展。在原子核处于满壳时，原子核趋于球形。当满壳以外存在核子时，满壳外的核子对于核心部分会产生极化作用，使之产生形变。满壳层内的核子的运动又有保持球对称的趋势，对于极化作用有一种恢复力。在一定的条件下，这两种作用达到平衡。