[科普中国]-类氢原子

类氢原子（hydrogen-like atom）是只拥有一个电子的原子，与氢原子同为等电子体，例如，He+, Li2+, Be3+与B4+等等都是类氢原子，又称为“类氢离子”。类氢原子只含有一个原子核与一个电子，是个简单的二体系统，系统内的作用力只跟二体之间的距离有关，是反平方连心力。这反平方连心力二体系统不需再加理想化，简单化。描述这系统的（非相对论性的）薛定谔方程式有解析解，也就是说，解答能以有限数量的常见函数来表达。满足这薛定谔方程式的波函数可以完全地描述电子的量子行为。在量子力学里，类氢原子问题是一个很简单，很实用，而又有解析解的问题。所推演出来的基本物理理论，又可以用简单的实验来核对。所以，类氢原子问题是个很重要的问题。

称满足上述系统的薛定谔方程式的波函数为单电子波函数，或类氢原子波函数。类氢原子波函数是单电子角动量算符 L 与其 z-轴分量算符 Lz的本征函数。由于能量本征值 E n 跟量子数 l，m 无关，而只跟主量子数 n 有关。所以，类氢原子波函数可以由主量子数 n 、角量子数 l 、磁量子数 m独特地决定。因为构造原理，还必须加上自旋量子数 m s = ± 1 / 2。对于多电子原子，这原理限制了电子构型的四个量子数。对于类氢原子，所有简并的轨域形成了一个电子层；每一个电子层都有其独特的主量子数 n．这主量子数决定了电子层的能量。

除了氢原子（电中性）以外，类氢原子都是离子，都带有正电荷量 e ( Z − 1 )；其中，e， Z 是原子序数。

薛定谔方程类氢原子问题的薛定谔方程式为1

−ℏ2/(2μ) ∇2ψ+V(r)ψ=Eψ

其中，ℏ 是约化普朗克常数，μ是电子与原子核的约化质量，ψ是量子态的波函数，E是能量，V(r)是库仑势：

V(r)=−Ze2/(4πϵ0r)

其中，ϵ0是真空电容率，Z是原子序数，e 是单位电荷量，r是电子离原子核的距离。

采用球坐标 (r,θ,ϕ)将拉普拉斯算子展开：

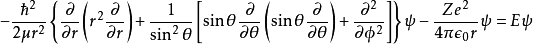
猜想这薛定谔方程式的波函数解 ψ(r,θ,ϕ)是径向函数 Rnl(r) 与球谐函数 Ylm(θ,ϕ)的乘积：

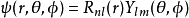
角向部分参数为天顶角和方位角的球谐函数，满足角部分方程式

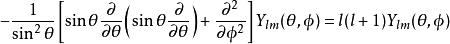
其中，非负整数 l是轨角动量的角量子数。磁量子数 m（满足 −l≤m≤l ）是轨角动量对于 z-轴的（量子化的）投影。不同的 l与 m给予不同的轨角动量函数解答 Ylm：

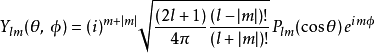
其中，i是虚数单位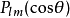， 是伴随勒让德多项式，用方程式定义为

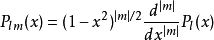
而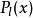 是 l阶勒让德多项式，可用罗德里格公式表示为

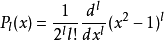
径向部分解答径向函数满足一个一维薛丁格方程式：

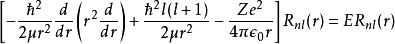
方程式左边的第二项可以视为离心力位势，其效应是将径向距离拉远一点。

除了量子数 ℓ 与 m以外，还有一个主量子数 n。为了满足 Rnl(r) 的边界条件，n必须是正值整数，能量也离散为能级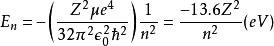 。随著量子数的不同，函数 Rnl(r)与 Ylm都会有对应的改变。按照惯例，规定用波函数的下标符号来表示这些量子数。这样，径向函数可以表达为

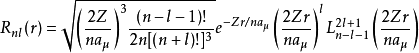
其中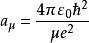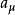，。 近似于波耳半径 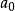。假若，原子核的质量是无限大的，则 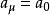，并且，约化质量等于电子的质量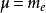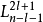，。是广义拉格耳多项式，定义为

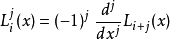
其中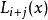，是拉格耳多项式，可用罗德里格公式表示为

其中l