[科普中国]-原子磁矩

介绍

原子磁矩（atomic magnetic moment）

原子内部各种磁矩总和的有效部分。一个原子的总磁矩，是其内部所有电子的轨道磁矩、自旋磁矩和核磁矩的矢量和。原子核具有磁矩，但核磁矩很小，通常可忽略，原子磁矩则为电子轨道磁矩与自旋磁矩的总和的有效部分 。

一般地原子磁矩μJ与原子的总角动量PJ有简单的关系，大小为μJ=g(e/2m)PJ，方向相反，式中e/m是电子的荷质比，g称为朗德g因子，它可以根据原子中的耦合类型计算出来，是表征原子磁性质的量。原子磁矩在塞曼效应中起重要作用。

磁矩定义描述载流线圈磁性质及微观粒子物理性质的物理量。载有电流I、面积为S的平面线圈的磁矩m定义为：

m=I×S×n；

式中，n为沿平面线圈法线方向的单位矢量，其指向与电流I环绕方向间成右螺旋关系，磁矩为m的载流小线圈在磁感应强度为B的磁场中受到的磁力F、磁力矩L分别为：F=(m×grad)×BL=MB

磁矩的单位为A·m2。电子磁矩的通用单位是 玻尔磁子(μB=9.274×1024A·m-2)。原子核、质 子和中子磁矩的类似单位是核磁子(相当于5.051 ×1027A·m2)。

电子磁矩原子磁矩来源于两部分，电子围绕核的轨道运动和电子的自旋。

从原子结构的简单模型出发，电子以角速度ω、半径为r作圆轨道运动时，它所产生的电流为-eω/2π。其中e为电子的电荷，若电流i闭合回路的截面积为S，那么从电磁理论可以得出，这时的磁矩为μ0iS(单位为Wb·m)。

因此由单个电子的圆周运动所产生的轨道磁矩为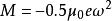：。其中e为电子电荷，ω为角速度。μo为真空磁导率

圆周运动的角动量为pl=mωr·r，其中m是电子的质量。因此， 轨道磁矩可改写成Ml= 实际上， 电子围绕原子核的运动是一量子效应， 按照量子力学， 角动量pl= ，这里l是轨道量子数，ћ为Planck常数被2π除。这样轨道磁矩Ml==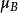，为Bohr磁子。

若原子中有多个电子，则总的轨道角动量等于各个电子轨道角动量的矢量和，即总轨道角动量等于PL=∑pl，其数值为pl=。这里L是总轨道角量子数，是l值的一定的组合。这样具有多个电子的原子的轨道磁矩为ML=。除了轨道磁矩外，自旋的电子也具有自旋磁矩。

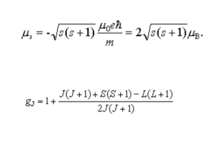
这些公式中，g——朗德因子（lande splitting factor）；J——原子总角量子数；L——原子总轨道角量子数；S——原子总自旋量子数。

若一个原子有多个电子，则总的自旋量子数也是各个电子自旋量子数的组合，总自旋角动量Ps=，总自旋磁矩μs=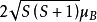。上面讨论了电子的轨道磁矩和自旋磁矩，对于大多数磁性原子，其原子的总磁矩可以通过LS耦合给出，即如上所述，原子中各电子的轨道角动量和自旋角动量各自分别合成总的轨道和自旋角动量，然后两者再合成原子的总角动量J=L+S。由于原子总磁矩MJ在磁场中的取向也是量子化的，所以M在外磁场方向上的分量MJZ=gJmJμB。

mJ有(2J+1)个可能取值，当mJ取最大值J时，就得到原子总磁矩在磁场方向上的最大分量，MJZ=gJJμB.这里gJ是Lande因子。上述LS耦合也称Russell-Saunders耦合，除了LS耦合外，尚有jj耦合。此时，各电子的轨道角动量和自旋角动量先合成电子的总角动量j，然后各电子的总角量j再合成原子的总角动量。jj耦合适用于原子序数大于Z=82的原子。2