空泡现象
水翼船的一个优势是具有较高的航速,但是在过高的速度下,水翼将产生空泡,空泡会使水翼的流体动力性能恶化,所以在设计中必须考虑空泡对水翼船性能的影响,对空泡进行校验,避免空泡的产生。
空泡的影响水翼在水中运动时,其表面压力发生变化,当水翼低压区的压力降低到临界值以下时,水开始汽化,产生空泡。一般认为,压力的l临界值即为该温度时水的汽化压力(或称饱和蒸汽压力)。
空泡发展过程分为三个阶段。在空泡的第一阶段,空泡区域是局部的,空泡在低压区形成,进入高压区以后,在水翼随边前面的表面处溃灭,对水翼的升力和阻力没有明显影响,但对水翼表面产生剥蚀。在空泡第二阶段,水翼上表面形成为一个很大的空泡腔,空泡在水翼的后方溃灭,对水翼表面不产生剥蚀作用,但使水翼的升力和阻力都下降。在空泡第三阶段,空泡腔覆盖了整个水翼,这时水翼的上表面全部被气泡覆盖,这种状态也称为全空泡状态。此状态下,由于湿面积减少,水翼升力和阻力均大幅下降。1
水翼空泡的校验检验空泡是否发生的标准就是翼背压力最低点是否达到该温度时的饱和蒸汽压,即pmin≤pd。
用无因次表示压降系数为
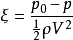
令产生空泡时的压力为pd,则定义空泡数
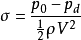
这时空泡产生的条件为
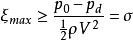
 只要最大压降系数大于等于空泡数,则水翼翼背就会产生空泡。
只要最大压降系数大于等于空泡数,则水翼翼背就会产生空泡。
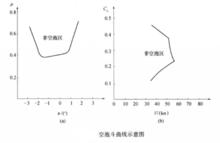
在设计水翼船时,可以通过空泡斗曲线得到不产生空泡的水翼工作区域。空泡斗曲线可以通过理论计算或试验得到,根据不同的设计需求其形式多样。有的显示水翼在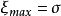 时所对应的水翼攻角和空泡数之间的关系曲线(图1(a)),有的通过水翼升力系数与航速之间的关系曲线来显示空泡界线(图1(b))。水翼船在空泡斗曲线边界线以内航行才能避免空化,在设计水翼时,需要加上一定的安全裕量。1
时所对应的水翼攻角和空泡数之间的关系曲线(图1(a)),有的通过水翼升力系数与航速之间的关系曲线来显示空泡界线(图1(b))。水翼船在空泡斗曲线边界线以内航行才能避免空化,在设计水翼时,需要加上一定的安全裕量。1
空泡螺旋桨计算的理论基础B.M.拉符伦基耶夫曾假设人们都知道,理想推进器理论使我们可以根据流体力学的一般定理确立诱导速度、推进器效率和推进器负荷系数之间的关系。如果作一假设,该假设反映了有空泡现象时推进器工作区域中的水流特点,就可以得到空泡推进器的类似的关系式。这些特点中的基本点是产生了空泡,它破坏了水流的连续性,并且增加了水流在叶片区域中的轴向速度。为了近似地反映这个特点,曾经设定了几个在空泡推进器区域中的简化了的水流流动图形。比如说B.M.拉符伦基耶夫曾假设,在空泡螺旋桨区有一与无穷远处水流垂直的平面,该平面上的压力是饱和水蒸汽的压力。这时利用伯努利方程可以得到空泡推进器近前方的临界流速
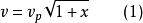
现在我们来研究两个等推力推进器,其中一个是有空泡现象发生的,而另一个是没有空泡现象发生。由下式确定上述推进器中每一个的推力值
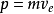 式中:m——流经推进器流管的任意截面的液体质量。
式中:m——流经推进器流管的任意截面的液体质量。
可以按下式确定m的数值
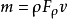
对于无空泡现象的螺旋桨,v由下列二项式表示

如果螺旋桨产生空泡现象,这个数值不应该大于按公式(1)所确定的v值。可能有这样的情况,即
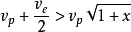
在这种情况下,流经无空泡现象的推进器盘面的液体质量将是
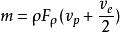
与此同时,流经有空泡影响之推进器盘面的液体质量将由下式表示
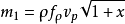 显然,如果
显然,如果
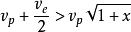
则
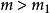
这样一来,就可以得出结论,等推力空泡推进器的诱导速度应该大于无空泡现象的推进器的诱导速度。因此空泡推进器的效率降低了。
B.M.拉符伦基耶夫曾经给出确定理想空泡推进器效率上界的关系式2
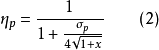
巴甫米尔方法巴甫米尔首先拟定了空泡螺旋桨计算的实用方法。按照这个方法,以下列方式验算处于空泡现象第二阶段的螺旋桨。首先假定螺旋桨上无空泡现象发生,并完成无空泡螺旋桨的验算。这种计算的结果确定了无空泡现象螺旋桨的推力系数与进速系数的关系。继而引进关于在固定的进速系数下,叶元体中的每一攻角不依赖空泡现象的发展,而保持常量的假设。此时螺旋桨的诱导速度也不依赖于螺旋桨是否发生空泡现象。上述假设使我们可以认为,叶元体的升力系数与单位推力系数之比是一个常量。
这个条件使巴甫米尔确立了在任意空泡数时的推力降低系数与对应于空泡现象极端发展时的推力降低系数间的关系。用下式表示这种关系
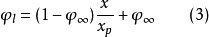 式中:
式中: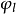 ——空泡螺旋桨的推力降低系数;
——空泡螺旋桨的推力降低系数;
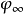 ——对应于空泡极端发展时的推力降低系数;
——对应于空泡极端发展时的推力降低系数;
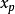 ——临界空泡数。
——临界空泡数。
巴甫米尔建议用下面的经验公式来确定计算所必须的数值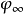 ,该公式是在分析整理空泡翼型风洞试验数据的基础上得到的。
,该公式是在分析整理空泡翼型风洞试验数据的基础上得到的。
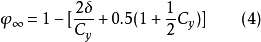
实践表明,对螺旋桨的工况有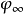 >0,因而,所研究的计算方法使得甚至当空泡数等于零时,螺旋桨的推力也是正的。
>0,因而,所研究的计算方法使得甚至当空泡数等于零时,螺旋桨的推力也是正的。
巴甫米尔认为叶元体的攻角不依赖空泡现象的发展,而是常量的假设,使得他所建议的这个计算方法不够严密。2
空泡螺旋桨验算程序下面给出了按巴甫米尔方法进行空泡螺旋桨验算的程序。
假设已知无空泡螺旋桨的关系式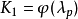 和
和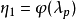 。给螺旋桨等值半径Re(假设在这个半径上的螺旋桨特性与整个螺旋桨的特性相同)确定升力系数的概略数值
。给螺旋桨等值半径Re(假设在这个半径上的螺旋桨特性与整个螺旋桨的特性相同)确定升力系数的概略数值
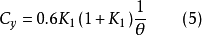
确定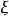 、
、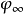 的近似值
的近似值
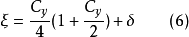
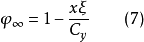
为了继续计算,必须给出空泡数x,然后按下式计算临界空泡数
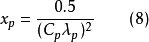 式中
式中

确定表征升力系数降低的系数
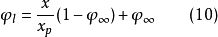 然后再确定推力系数
然后再确定推力系数
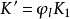
巴甫米尔建议采用下面的经验公式确定表征在发生空泡现象时’的力矩系数降低的系数2
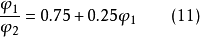
H.H.波良霍夫研究后来,H.H.波良霍夫依据空泡区在离空泡螺旋桨叶片有限距离上就闭合的条件,研究了应用于空泡螺旋桨力学的一般理论。在这里利用了动量守恒原理和动能定理,他得到了螺旋桨理论的普通公式
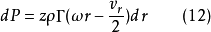
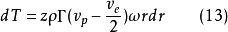
研究这些公式,我们可以得出结论,不管是对于空泡螺旋桨,还是对于无空泡螺旋桨,总可以给它找到那样一个直线形涡线的支承系统,这个系统所形成的自由涡系与螺旋桨形成的自由涡系一样,并且给出与螺旋桨一样的拉力和功率数值。
然后,H.H.波良霍夫在公式(12)和(13)的基础上作出结论,既然空泡螺旋桨和无空泡螺旋桨在相同的几何攻角下,其叶元体的升力系数不同,那么这些螺旋桨的诱导速度也将是互不相同的。
实际上,H.H.波良霍夫建议在设计空泡螺旋桨时,使用无空泡螺旋桨的一般关系式,只是应该注意到,在计算里必须引进空泡翼型的Cx和Cy的数值。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国