影响因素重力固体潮
重力固体潮主要来自于日、月天体(非常微小的部分来自于离地球较近的行星)的引潮力的作用,是地表重力时间变化的主要成份。采用现代天文观测技术获得的太阳、月亮和行星的精密轨道参数,可以获得精确的引潮位展开表。因此,一方面,根据描述地球弹性及其对引潮力响应特征的Love数和各类体潮的潮汐参数,可以从理论上预测出重力固体潮。研究表明,由于近周日共振的影响,周日频段的固体潮潮汐参数表现出非常显著的频率依赖特征;对于任何潮波,重力潮汐参数可以表示为全球常数项和相对极其微小的纬度依赖项之和。在固体潮理论模拟中,已逐步顾及到地球的自转、椭率、地幔的非弹性、侧向(密度)非均匀性及(弹性)各向异性等特征。研究表明,侧向非均匀性和各向异性对固体潮的影响很小,在目前的技术条件下无法在实际观测结果中反映出来。同时,必须看到,这些理论模拟结果都是基于流体静力平衡假设获得的,这一假设将直导致采用的液核动 力学椭率偏小约5%,从而导致重力潮汐,特别是周日潮汐模拟计算结果存在比较大的偏差;为此,科学家避免了流体静力平衡假设,采用实际观测资料修正液核动力学椭率,获得更精确的重力潮汐理论模型。另一方面,重力固体潮可以通过高精度重力仪在地表的长期连续观测获得。观测结果表明,随着观测技术的提高,特别是超导重力仪和 LaCoste-ET 弹簧重力仪在全球范围内的普遍使用和观测资料的长期积累,重力固体潮的观测精度已经非常高;目前的重力潮汐理论模型可以很好地解释观测结果,特别是超导重力仪观测结果,二者在主要潮波的差异优于0.5%。采用全球超导重力仪长期连续观测资料,考虑周日潮汐的近周日共振特征,建立了高精度的重力潮汐全球实测模型。1
海洋潮汐的负荷效应海潮的负荷(OTL)效应是地表潮汐观测和潮汐理论模拟之间差异的主要来源,由于海潮和固体潮具有相同的力源和类似的频谱特征,只能采用表面负荷理论和已有的海潮模型,通过表面负荷 Green函数与海潮潮高的全球褶积从理论上计算出海潮的负荷影响。1980年,Schwiderski采用大量验潮站资料和潮汐运动方程,建立了第一个全球海潮模型。随着卫星测高资料的积累及数值计算技术的发展,特别是有限元数值计算方法的应用,获得了 许多精度和分辨率更高的全球海潮模型。大量地表重力潮汐观测结果表明,尽管目前全球海潮模型的精度和空间分辨率存在着差异,但是对负荷效应的模拟计算结果影响甚微,在目前的观测精度以内。对于中国大陆,局部海域的海潮负荷对重力观测,特别是沿海地区重力观测的影响极其显著,中国大陆具有很长的海岸线,要建立中国大陆精密的重力潮汐改正模型必须顾及局部近海海潮运动特征。
采用理论或实验固体潮模型、海潮负荷效应,可以精确合成重力观测中的潮汐变化,为连续、流动和绝对重 力观测提供精密的潮汐改正模型。
改正方法重力固体潮模型改正对于某个地球模型,采用合理的数值积分方法,解算地球潮汐运动方程,获得重力潮汐参数。由于地球自转和椭率,二阶重力潮汐参数可以表示为常数项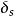 和微小的纬度依赖项
和微小的纬度依赖项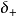 、
、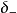 之和。事实上,地球的高阶重力潮汐参数也存在纬度依赖项,但由于地球的潮汐形变最主要的部分是二阶项,高阶潮汐信号相对较小,且纬度依赖项非常微弱,在现有观测技术条件下可忽略。Dehant等学者采用分层(包括地幔、内外核、不包含大气和海洋)、自转、微椭、非弹性地球模型和非流体静力平衡的地球模型,考虑了内部的椭率对密度、剪切和压缩模量、重力位以及边界地形的影响,为了使得计算得到的理论自由核章动(FCN)周期接近于观测值,考虑了地幔的对流和非弹性,理论模拟了重力潮汐参数 (模 型 记 为 DDW99)。Mathews等学者采用基于 VLBI观测获得的FCN 周期,修正了 PREM 模型的液核和地球的动力学扁率,并将 Love数和重力潮汐参数描述为若干旋转简正模共振之和的形式,获得了另一个精确的重力潮汐理论模型 (记为 M2001)。与以前的同类研究结果相比,由于这两个模型采用实际观测的FCN 周期修正液核的动力学扁率,从客观上避免了流体静力平衡近似,由此获得的重力潮汐参数更客观地描述了近周日共振特征,被认为是目前最精确的两个潮汐理论模型.
之和。事实上,地球的高阶重力潮汐参数也存在纬度依赖项,但由于地球的潮汐形变最主要的部分是二阶项,高阶潮汐信号相对较小,且纬度依赖项非常微弱,在现有观测技术条件下可忽略。Dehant等学者采用分层(包括地幔、内外核、不包含大气和海洋)、自转、微椭、非弹性地球模型和非流体静力平衡的地球模型,考虑了内部的椭率对密度、剪切和压缩模量、重力位以及边界地形的影响,为了使得计算得到的理论自由核章动(FCN)周期接近于观测值,考虑了地幔的对流和非弹性,理论模拟了重力潮汐参数 (模 型 记 为 DDW99)。Mathews等学者采用基于 VLBI观测获得的FCN 周期,修正了 PREM 模型的液核和地球的动力学扁率,并将 Love数和重力潮汐参数描述为若干旋转简正模共振之和的形式,获得了另一个精确的重力潮汐理论模型 (记为 M2001)。与以前的同类研究结果相比,由于这两个模型采用实际观测的FCN 周期修正液核的动力学扁率,从客观上避免了流体静力平衡近似,由此获得的重力潮汐参数更客观地描述了近周日共振特征,被认为是目前最精确的两个潮汐理论模型.
海潮负荷模型改正目前的研究表明 不同全球海潮模型在远海区比较一致,而差别主要反应在沿海地区,因此为了提高沿海测点的海潮负荷计算精度,远区可采用 NAO99 (网格0.5°×0.5°)全球海潮模型,近区可采用 Fang等学者提供的中国近海潮汐资料。海潮负荷影响主要在沿海地区,海潮负荷影响在南部沿海区域为最大, 达到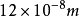 ·
·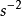 ,在其他沿海区域也在
,在其他沿海区域也在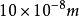 ·
·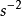 左右,其中局部近海潮汐的影响约占 10%,次要潮波的影响约占3%,在高精度重力测量 中都有必要充分考虑;随着离海岸线距离的增加,海潮负荷的影响逐步减小。
左右,其中局部近海潮汐的影响约占 10%,次要潮波的影响约占3%,在高精度重力测量 中都有必要充分考虑;随着离海岸线距离的增加,海潮负荷的影响逐步减小。
重力潮汐改正模型模型的建立重力潮汐包含了固体地球的潮汐以及由海洋潮汐引起的负荷潮汐,并耦合在实际的重力观测中(如相对和绝对重力测量),因此重力观测资料中的潮汐改正就是扣除这两部分的影响.固体潮模型给出的是频率域各潮波的潮汐参数,也就是潮波的振幅与刚体地球潮波振幅的比值以及潮波的相位与刚体地球潮波的相位之间的差值。潮波的振幅总是正的,由于海潮模型给出的潮高和相位不包含类似于固体潮中的大地系数的量,因此所计算的海潮负荷也没有与大地系数有关的项,而固体潮计算中的大地系数在不同的纬度地区有正负之分,最后用振幅和相位来表示将导致相位180°的偏移,因此在将海潮负荷和固体潮模型值叠加时需考虑由此引起的相位的改正,不同纬度区的相位改正值可参考文献。因此,对于中国及周边地区,只有长周期潮汐存在相位改正的问题,即在纬度大 于 35.26°的 地 区 要 加 上180°的相位改正。因此最后潮汐改正所用的潮汐参数就是综合固体潮模型值和海潮负荷值:

式中 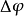 为相位改正值。由于三阶和四阶的固体潮潮波振幅很小,因此只有二阶的潮波加上了海潮负荷的影响,也就是说在某一个波群中,二阶的潮波采用顾及海潮负荷影响的潮汐参数,而三阶和四阶的潮波采用理论的潮汐参数。对于中国大陆任何测点,采用理论或实验模型(DDW99,M2001)即可获得重力潮汐参数;根据海潮模型(包括 NAO99,FES04 和中国近海海潮图)提供的各主要潮波的等潮图(振幅和相位),根据表面负荷理论计算它们的负荷效应,然后利用上式对潮波的重力潮汐参数进行修正;
为相位改正值。由于三阶和四阶的固体潮潮波振幅很小,因此只有二阶的潮波加上了海潮负荷的影响,也就是说在某一个波群中,二阶的潮波采用顾及海潮负荷影响的潮汐参数,而三阶和四阶的潮波采用理论的潮汐参数。对于中国大陆任何测点,采用理论或实验模型(DDW99,M2001)即可获得重力潮汐参数;根据海潮模型(包括 NAO99,FES04 和中国近海海潮图)提供的各主要潮波的等潮图(振幅和相位),根据表面负荷理论计算它们的负荷效应,然后利用上式对潮波的重力潮汐参数进行修正;
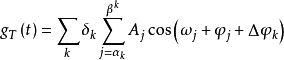

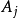 式中t为参考时间,
式中t为参考时间,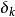 和
和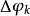 为第k个潮汐波群的振幅因子和相位差(统称重力潮汐参数);
为第k个潮汐波群的振幅因子和相位差(统称重力潮汐参数);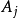 、
、 、
、
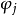 分别为第j个潮波的理论振幅、角频率和初始相位,根据引潮位展开表获得,其中(大地系数与相对振幅的乘积的绝对值)具有极强的纬度依赖特征,为天体轨道参数一阶导数的线性组合;
分别为第j个潮波的理论振幅、角频率和初始相位,根据引潮位展开表获得,其中(大地系数与相对振幅的乘积的绝对值)具有极强的纬度依赖特征,为天体轨道参数一阶导数的线性组合;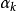 和
和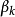 为第k个潮汐波群在引潮位展开表中的始末位置。
为第k个潮汐波群在引潮位展开表中的始末位置。
最后利用上述方程就可以获得该测点的潮汐改正值,从而获得中国大陆的重力潮汐改正模型。海潮负荷使得中国大陆,特别在沿海区域重力潮汐的影响幅度的形态发生了显著的变化,海潮负荷影响最大的位于南部沿海区域,且随着离海岸线距离的增加,影响逐渐减小。
模型的精度分析采用 DDW99固体潮模型和海潮负荷对武汉台超导重力仪连续观测作重力潮汐改正,分析表明经重力潮汐改正后,超导重力仪观测与局部气压变化存在极强的相关性,重力变化来源主要是局部的环境变化,如果扣除局部气压的影响和长期趋势项,基本上不包含重力潮汐变化或潮汐信号非常微弱,其均方差仅为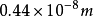 ·
·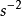 。
。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国