[科普中国]-透视投影

简介

透视投影是用中心投影法将形体投射到投影面上，从而获得的一种较为接近视觉效果的单面投影图。它具有消失感、距离感、相同大小的形体呈现出有规律的变化等一系列的透视特性，能逼真地反映形体的空间形象。

透视投影符合人们心理习惯，即离视点近的物体大，离视点远的物体小，远到极点即为消失，成为灭点。它的视景体类似于一个顶部和底部都被切除掉的棱椎，也就是棱台。这个投影通常用于动画、视觉仿真以及其它许多具有真实性反映的方面。

现实生活中的景物，由于观察距离及方位的不同在视觉上会引起不同的反映，这种现象就是透视现象。研究透视现象并使之能在平面上用线来表现其规律，使画面可正确地表现出物体远近之间的层次关系，使观察者获得立体、有深度的空间感觉，就必须研究透视变换的规律。1

投影投影变换是在世界坐标系中建立的，而计算机屏幕所显示的图形是在给定视点和视线方向下的二维屏幕投影。所以投影变换是整个图形变换的关键。根据投影中心与投影平面之间距离的不同，投影可分为透视投影和正射投影。

透视投影类似于人对客观世界的观察方式，它的特点是距离视点近的物体比较大，而距离远的物体相对比较小，这种投影方式的视景空间可以被认为是一个棱台。它广泛应用于三维地形模拟、飞行穿越仿真、步行穿越仿真等模拟人眼视觉效果的研究领域。

正射投影是物体直接映射到屏幕上。正射投影实质上是透视投影的一种特例，即视点在无穷远或视点由一个点变为一个面。它适用于某地的顶视效果图、地形晕渲图或需要观察模型某一个侧面不带有形变的景观等。2

透视图绘制方法利用计算机绘制或显示物体的透视图，常采用图形变换的矩阵方法。一般是按下列两种方法来获得物体透视图。按透视变换的矩阵方法作透视图时，画面必须是空间透射变换的二重面，即透射轴平面，否则得到的将不是透视投影，而只是一个经各种变换后得到的二维图形。

1、把物体平移到适当位置后，进行射影变换，然后绕坐标轴旋转，最后向某一坐标面进行正投影。

2、把物体平移到适当位置后，进行绕坐标轴的旋转变换，然后施以射影变换，最后向某一坐标面进行正投影。

然而，不论采用哪种方法，得到的图形常会出现较大的变形。其原因，除开采用这些方法时难于较好地选定物体、画面和视点的相对位置外，更主要的是运用这些方法有时不能得到真正的透视图。3

空间透射相关定义空间透射空间透射(Stereohomology)——从空间场k1到k2的广义射影变换T，若变换存在一个不动点的轨迹平面(称之为界面），且对任意点P∈k1及其对应点P'∈k2存在一固定点S(称之为透射中心)与PP'共线。则称T是从k1到k2的空间透射变换。4

空间透视空间透视(Stereoperspective)——是透射中心S在界面c上且皆为固有元素的满秩空间透射变换。4

中心投影中心投影(CentralProjection)——是透射中心S为可及点(亦即固有点)，界面c为可及平面(亦即固有平面)的降秩空间透射变换。4

平行投影平行投影(ParallelProjection)——是透射中心S为不可及点(非固有点)而界面c为可及(固有)平面的降秩空间透射变换。4

平移变换平移变换(TranslationTransformation)——是透射中心S及界面c皆非固有元素的满秩空间透射变换。4

中心辐射相似变换中心辐射相似变换(CentralRadiationSimilarTransformation)——是透射中心S为固有点而界面c为非固有平面的满秩空间透射。4

透视投影矩阵变换投影变换是图形变换的关键内容，是联系三维空间物体与二维屏幕图形的桥梁。在三维图形显示中，一般采用透视投影变换，其变换矩阵也有多种形式。

过渡坐标系透视投影的视线（投影线）是从视点（观察点）出发，视线是不平行的。透视投影按主灭点个数分为一点透视、二点透视和三点透视，任何一束不平行于投影平面的透视投影将汇聚成一点，称之为灭点，在坐标轴上的灭点称为主灭点。

三维图形显示采用的投影一般为一点透视投影，在简单一点透视投影变换中，由于投影平面取成坐标系中的一个坐标平面，因此用一个坐标系即可表示透视投影变换，如图。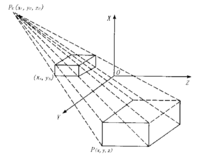

在透视投影中往往要求物体不动，让视点在以形体为中心的球面上变化来观察形体各个方向上的形象，解决的办法是引入一个过渡坐标系，即视点坐标系。

视点坐标系是左手三维直角坐标系，与一般物体所在的世界坐标系不同，是以人眼为坐标原点，坐标轴遵循左手法则，即左手大拇指指向Z轴的正方向，与之垂直的4个手指指向X轴的正方向，四指弯曲成90°的方向是Y轴的正方向。2

实现矩阵变换引入了过渡坐标系后，透视投影变换可看作是两个基本变换，即世界坐标系到视点坐标系的变换和视点坐标系到屏幕坐标系的变换。变换矩阵有如下五步：

（1）将世界坐标系的原点平移到视点

（2）令平移后的新坐标轴绕X'轴旋转90°，则形体上的点是顺转90°。

（3）将新坐标系绕y'顺时针转θ角，此时θ角大于180°，形体顶点逆转θ角。

（4）再令新坐标系绕x'顺时针转φ角，形体顶点逆转φ。

（5）右手坐标系变成左手坐标系，Z轴反向。2