[科普中国]-卡夫拉伊斯基任意伪圆柱投影

概念

卡夫拉伊斯基任意伪圆柱投影又称“卡夫拉伊斯基椭圆投影”。属非等面积的伪圆柱投影。由苏联卡夫拉伊斯基教授拟定，故名。这个投影图上的纬线是一组平行直线，中央经线为直线并与纬线直交并与实地等长，其他经线为对称于中央经线的椭圆，其中一条经线为圆。若把长度比等于1的纬线取在35°31′34″处，以圆表示的一条经线在土120°处，则投影效果为最佳。此投影结构简单，经线曲率不大，计算比较方便，可用于绘制世界地图。

地图投影按照一定的数学法则将地球椭球面上的经纬线转移到平面上的方法。也就是使地球椭球面上各点的地理坐标与平面上各点的直角坐标(或极坐标)保持一定的函数关系。地球椭球面是曲面，而地图是绘制在平面上，因此制图时首先要把曲面展为平面。然而地球椭球面是个不可展的曲面，假如把它直接展为平面，必然发生破裂或褶皱，用这种具有破裂或褶皱的平面绘制地图，显然是不实用的。所以必须采用数学方法将曲面展为平面，以保持平面上图形的完整和连续。地图投影方法很多，但不论采用什么投影方法所得到的经纬线网形状都不可能与地球椭球面上的经纬线网形状完全相似。这表明投影之后地图上的经纬线网发生了变形，因而根据地理坐标展绘在地图上的各种地理事物也必然随之产生变形。变形主要表现在三个方面： 长度变形、面积变形和角度变形。变形是不可避免的，但若给予一定的条件，如等角条件，等积条件，则可使其中某种变形等于零，用以满足不同用途对地图投影的要求。按变形性质地图投影可分为三类： 等角投影、等积投影和任意投影(包括等距投影)。

地图投影最初建立在透视的几何原理上，它是把地球椭球面直接透视到平面上，或透视到可展为平面的曲面上，如圆柱面和圆锥面。这样就得到具有几何意义的方位、圆柱和圆锥投影。随着科学的发展，为了使地图上变形尽量减小，或者为了使地图满足某些特定要求，地图投影逐渐跳出了原来借助几何面构成投影的框子，而产生了一系列按照数学条件构成的投影。按照构成方法可以把地图投影分为两大类： 几何投影和非几何投影。几何投影是把地球椭球面上的经纬线投影到几何面上，然后将几何面展为平面而成的。根据几何面的形状可以分为方位投影、圆柱投影和圆锥投影。非几何投影是不借助于几何面，根据某些条件用数学解析法确定地球椭球面与平面之间点与点的函数关系。在这类投影中，一般按经纬线形状又分为伪方位投影、伪圆柱投影、伪圆锥投影和多圆锥投影。1

圆柱投影以圆柱面作为投影面，使圆柱面与地球相切或相割，将地球面上的经纬线投影到圆柱面上，然后把圆柱面沿一条母线剪开展为平面而成。由于圆柱面与地球相切或相割的位置不同，有正轴圆柱投影、横轴圆柱投影和斜轴圆柱投影。正轴圆柱投影是圆柱的轴与地轴重合，横轴圆柱投影是圆柱的轴与地轴垂直，斜轴圆柱投影是圆柱的轴与地轴斜交。正轴圆柱投影的经纬线形状比较简单，称为标准网。纬线为平行直线，经线为与纬线垂直且间隔相等的平行直线。在这类投影图上任意一点的位置是用直角坐标表示的。设以某一条经线为X轴，赤道为Y轴，由于纬线投影为平行于赤道的直线，所以X坐标仅依纬度的变化而变化，即X是纬度q的函数，一般用X=f(q)式表达。经线为与赤道垂直的平行直线，经线间的间隔与相应的经差λ成正比，故Y坐标与经差成正比，即y=cλ(c—常数)。因此正轴圆柱投影的一般公式为：

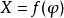
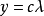
c值由切圆柱或割圆柱的条件决定。由于决定x函数形式的方法不同，有等角圆柱投影、等积圆柱投影和任意(包括等距)圆柱投影。无论哪一种圆柱投影，其变形分布有着大致相同的规律。凡是切圆柱投影，赤道是一条没有变形的线，亦称标准纬线。从标准纬线向北、向南变形逐渐增大;凡是割圆柱投影，相割的两条纬线没有变形，是两条标准纬线，离标准纬线愈远，变形愈大。等变形线与纬线平行，呈平行线状分布。圆柱投影适宜绘制赤道附近和沿赤道两侧呈东西方向延伸地区的地图。

在圆柱投影中应用比较广泛的是正轴等角圆柱投影，又名墨卡托投影。在这个投影图上赤道是标准纬线，其他各纬线的长度比均大于1。为了保持等角特性，任一点的经线长度比均等于该点的纬线长度比，因此除赤道处经线长度比等于1之外，其他地方的经线长度比也随纬度的增加而增大。例如在纬度60°地方，纬线与经线的长度比均为2，纬度80°地方，经线和纬线长度比均等于5.7。由于经线长度比随纬度增高而增大，故图上纬线间隔从赤道向两极逐渐增大。极地不能表示出来。

墨卡托投影具有一个很重要的特性，就是把等角航线(又称斜航线)表现为直线，所以它在编制航海图和航空图中被广泛采用。例如我国编绘比例尺小于1∶2.5万的海图采用的是这个投影。此外，由于这个投影在低纬度地区变形小，而且经纬线形状简单，常用于绘制赤道附近的分国地图。例如我国地图出版社出版的一整套分国地图中，沿赤道的分区地图均采用这个投影。

伪圆柱投影伪圆柱投影又称“拟圆柱投影”。地图投影的一类。在圆柱投影基础上，按一定条件修改而成。正轴投影中，纬线为相互平行的直线，但不等长；中央经线为垂直于纬线的直线;其他经线为对称于中央经线的曲线；两极表现为点或线的图形。这类投影的经线与纬线不正交，故无等角性质的投影。多用等积伪圆柱投影编绘大区域地图，如世界图、大洋图和分洲图等。通常指定经线为某种曲线，即可求出特定的伪圆柱投影。

任意投影任意投影是既不等角又不等积的投影。在这种投影图上长度变形、面积变形和角度变形同时存在。在任意投影中有一种比较常见的等距投影。它是在某些特定方向上没有长度变形。例如在经纬线投影后为正交的投影中，沿经线方向长度没有变形，即m=1(m——经线长度比)，或是在图上从中心向外沿半径方向长度没有变形。等距投影的面积变形小于等角投影，角度变形小于等积投影。任意投影多用于要求面积变形不大，角度变形也不大的地图。如一般参考用图和教学用图。2

任意伪圆柱投影任意伪圆柱投影属非等面积性质的伪圆柱投影。由于所给条件不同，可导出各种形式的任意伪圆柱投影。常见的有乌尔马耶夫任意伪圆柱投影、卡夫拉伊斯基任意伪圆柱投影等。这类投影图上角度变形较等面积伪圆柱投影稍小，可用于绘制世界地图。

乌尔马耶夫任意伪圆柱投影乌尔马耶夫任意伪圆柱投影属非等面积伪圆柱投影中的一种。由苏联乌尔马耶夫(урмаев)为绘制太平洋地图设计的专用投影，故名。其纬线为一组平行直线，中央经线为直线并与纬线直交，其他经线为对称于中央经线的曲线。面积变形线与纬线平行，无角度变形点在中央经线与士51°纬线相交处，由此点向外角度变形增大，角度等变形线的形状和太平洋的轮廓基本一致。多用于太平洋图或太平洋—印度洋地图，中国1972年出版的世界地图集中曾采用这个投影。3