[科普中国]-透视旋转定律

定律定义

也称沙尔定律。

空间透视作图有助于建立空间概念，为了显示出透视对应图形的真实形状，可将相互透视的两个平面展开或叠合到一个平面上。如图所示，如果将物面绕透视轴旋转，而合面，绕合线气气按同一方向旋转相同的任意角度，保持这两个面的平行性，则像面和物面的透视对应关系仍然保持不变，投射线总是通过物面和像面上同一对应点，这一规律就是透视旋转定律。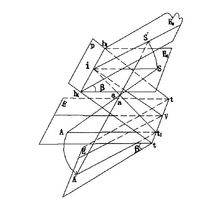

沙尔定律对旋转角度并无任何限制，将E平面和Es平面（如图）旋转到某一极限位置，使E平面和Es平面与像平面P叠合在一起，成为叠合图形。下图中表示E平面上有一个正方形，其对角线与基本方向线的夹角为45度，两对角线的合点分别为i1和i2，则ii1=ii2=Si，其中i为主合点。1

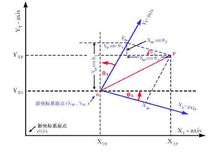
相关概念仿射变换（Affine Transformation）是空间直角坐标系的变换，从一个二维坐标变换到另一个二维坐标，仿射变换是一个线性变换，他保持了图像的“平行性”和“平直性”，即图像中原来的直线和平行线，变换后仍然保持原来的直线和平行线，仿射变换比较常用的特殊变换有平移(Translation)、缩放（Scale）、翻转（Flip）、旋转（Rotation）和剪切(Shear)。仿射变换也可以看成坐标系的旋转和缩放以及平移：（如图）

仿射变换：二维空间的变换 ； 线性变换 ；已知3对坐标点就可以求得变换矩阵。

透视变换：三维空间的变换 ； 非线性变换 ；已知4对坐标点可以求得变换矩阵。22

定律应用建筑物立面影像几何纠正

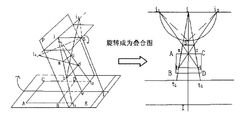
大多数建筑物上都存在着丰富的“平行线”信息，如下图中窗户的水平和垂直边缘线。利用这些表面的平行线作为初始解算条件，在透视旋转定律的基础上可以对建筑物立面纹理图像进行快速几何纠正，具体实现过程如下：

如右图所示，J，L，K，M为建筑物上的4个角点，其中JK与LM，JK与LM相互平行。利用透视旋转定律,得到其影像的叠合图如下。

依照同样的方法，可获得建筑物上其他任意点的构像。此算法简单易行，可快速纠正建筑物立面纹理影像。11

图像处理

利用透视中心、像点、目标点三点共线的条件，按透视旋转定律使承影面（透视面）绕迹线（透视轴）旋转某一角度，破坏原有的投影光线束，仍能保持承影面上投影几何图形不变的变换。