[科普中国]-循环队列

为充分利用向量空间，克服"假溢出"现象的方法是：将向量空间想象为一个首尾相接的圆环，并称这种向量为循环向量。存储在其中的队列称为循环队列（Circular Queue）。循环队列是把顺序队列首尾相连，把存储队列元素的表从逻辑上看成一个环，成为循环队列。

简介循环队列就是将队列存储空间的最后一个位置绕到第一个位置，形成逻辑上的环状空间，供队列循环使用。在循环队列结构中，当存储空间的最后一个位置已被使用而再要进入队运算时，只需要存储空间的第一个位置空闲，便可将元素加入到第一个位置，即将存储空间的第一个位置作为队尾。1循环队列可以更简单防止伪溢出的发生，但队列大小是固定的。

在循环队列中，当队列为空时，有front=rear，而当所有队列空间全占满时，也有front=rear。为了区别这两种情况，规定循环队列最多只能有MaxSize-1个队列元素，当循环队列中只剩下一个空存储单元时，队列就已经满了。因此，队列判空的条件时front=rear，而队列判满的条件时front=（rear+1）%MaxSize。2

基本操作// 队列的顺序存储结构(循环队列)#define MAX_QSIZE 5 // 最大队列长度+1typedef struct { int *base; // 初始化的动态分配存储空间 int front; // 头指针，若队列不空，指向队列头元素 int rear; // 尾指针，若队列不空，指向队列尾元素的下一个位置} SqQueue;// 构造一个空队列QSqQueue* Q_Init() { SqQueue *Q = (SqQueue*)malloc(sizeof(SqQueue)); // 存储分配失败 if (!Q){ exit(OVERFLOW); } Q->base = (int *)malloc(MAX_QSIZE * sizeof(int)); // 存储分配失败 if (!Q->base){ exit(OVERFLOW); } Q->front = Q->rear = 0; return Q;}// 销毁队列Q，Q不再存在void Q_Destroy(SqQueue *Q) { if (Q->base) free(Q->base); Q->base = NULL; Q->front = Q->rear = 0; free(Q);}// 将Q清为空队列void Q_Clear(SqQueue *Q) { Q->front = Q->rear = 0;}// 若队列Q为空队列，则返回1；否则返回-1int Q_Empty(SqQueue Q) { if (Q.front == Q.rear) // 队列空的标志 return 1; else return -1;}// 返回Q的元素个数，即队列的长度int Q_Length(SqQueue Q) { return (Q.rear - Q.front + MAX_QSIZE) % MAX_QSIZE;}// 若队列不空，则用e返回Q的队头元素，并返回OK；否则返回ERRORint Q_GetHead(SqQueue Q, int &e) { if (Q.front == Q.rear) // 队列空 return -1; e = Q.base[Q.front]; return 1;}// 打印队列中的内容void Q_Print(SqQueue Q) { int p = Q.front; while (Q.rear != p) { cout rear] = e; Q->rear = (Q->rear + 1) % MAX_QSIZE; return 1;}// 若队列不空，则删除Q的队头元素，用e返回其值，并返回1；否则返回-1int Q_Poll(SqQueue *Q, int &e) { if (Q->front == Q->rear) // 队列空 return -1; e = Q->base[Q->front]; Q->front = (Q->front + 1) % MAX_QSIZE; return 1;}条件处理循环队列中，由于入队时尾指针向前追赶头指针；出队时头指针向前追赶尾指针，造成队空和队满时头尾指针均相等。因此，无法通过条件front==rear来判别队列是"空"还是"满"。

解决这个问题的方法至少有两种：

① 另设一布尔变量以区别队列的空和满；

②另一种方式就是数据结构常用的： 队满时：(rear+1)%n==front，n为队列长度（所用数组大小），由于rear，front均为所用空间的指针，循环只是逻辑上的循环，所以需要求余运算。如图情况，队已满，但是rear（5）+1=6！=front（0），对空间长度求余，作用就在此6%6=0=front（0）。

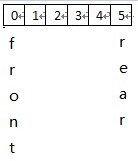
类型定义采用环状模型来实现队列,各数据成员的意义如下：

front指定队首位置，删除一个元素就将front顺时针移动一位；

rear指向元素要插入的位置，插入一个元素就将rear顺时针移动一位；

count存放队列中元素的个数，当count等于MaxQSize时，不可再向队列中插入元素。

队列数据结构分为线性结构和非线性结构，队列和线性表都是线性结构。线性表是由n 个数据元素组成的有限序列，该序列有惟一的“第一个”和惟一的“最后一个”数据元素；除了 “第一个”和“最后一个”之外，序列中的每个数据元素都只有一个直接前驱和一个直接后继。线性表的插入和删除操作可以在表中任意位置进行。队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。队列中没有元素时，称为空队列。

队列的数据元素又称为队列元素。在队列中插入一个队列元素称为入队，从队列中删除一个队列元素称为出队。因为队列只允许在一端插入，在另一端删除，所以只有最早进入队列的元素才能最先从队列中删除，故队列又称为先进先出（FIFO—first in first out）线性表。

本词条内容贡献者为:

徐恒山 - 讲师 - 西北农林科技大学