[科普中国]-卡皮查热阻

介绍

界面热阻的想法早在1936年就已经提出，在那之前，人们通常认为接触热阻很小，并不考虑。Keesom等人在1936年提出，接触界面的热阻有可能会非常大，但是没有仔细研究。在1941年，Kapitza 发表了他关于固体和液氦接触界面上存在温度降的实验研究，也因此，界面热阻又命名为Kapitza热阻1。

原理界面热阻产生的主要原因是由于处于接触的两种物质的电子特性以及振动特性不相同。当载热子（声子或者电子，视物质特性而定）试图穿过接触界面时，会发生散射。散射后的载热子的运动情况就完全取决于接触界面物质可用的能量状态。

假设穿过界面热流恒定，界面热阻会导致接触界面的温度降，根据傅立叶定律，有以下表达式：

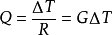Q : 接触界面的热流密度 R : 界面热阻 G: 热导系数

对于固体和液氦之间，以及金属和电介质之间及两电介质之间（紧密接触情况下）的界面来说，它们之间的热导主要靠声子传热，声子通过液氦到达固液界面时，发生反射或折射，遵守sinα1/sinαs=v1/vs，由于固体中的声速vs比液体中声速v1大得多，所以临界角αlc就很小，即只有很小的立体角范围内的声子有可能进入固体，同时固体和液氦的密度相差很大，声速相差也很大造成失匹配。

因此，只有能量小于10-5的一部分声子可以进入固体，所传输的能量也就很小了，在界面上传输能量的减小即出现了卡皮查热阻。

公式在低普朗特准则(Pr)物质的 蒸汽与冷却竖壁之间的膜状凝结对流换热计算中，所需计及的一项附加对流换热热阻。因此项热阻产生于汽-液两相分界面之上，故名界面热阻。常用符号 “Rp”表示，单位为“(m· ℃)/W”。其数学表达式为： Rp=(ts-ti) /q=Ra，t-Rλ，l。

式中，ts为蒸汽相应压力下的饱和温度(℃)；ti为汽-液界面上的真实温度 (℃)；q为膜状凝结时的对流换热热流密度(W/m)；Ra，t为由蒸汽到冷却壁面的总的对流换热热阻 [(m·℃)/W]；Rλ，l为由凝结液膜所构成的导热热阻[(m·℃)/W]。

实验研究表明，对于低Pr介质来说，总是存在界面热阻，且随着其值的增大，出现于汽-液界面上的 “温度跳跃”现象也愈显著，即界面上的真实温度比饱和温度低得愈多。2

作用卡皮查热阻的大小和固体表面情况有关对表面机械损伤特别敏感。理解物质之间的界面热阻，对于电子产品的设计尤为重要，这是因为在现今的电子器件中有非常多的接触界面，这会影响电子器件的散热。界面热阻在纳米尺度下更为重要，这是因为，在纳米尺度下，接触界面更多也更复杂。