[科普中国]-抽象语言族

定义

某些代数运算下具有封闭性的形式语言类,简称AFL。抽象语言族是用代数方法研究形式语言理论的重要成果。
基本定义 令∞为无限字母表，在其任一有限子集i上构造语言。如果任何一组语言{Li}中至少包含一个，则称{Li}为一语言族。
在同态、逆同态和与正则语言相交下保持封闭的语言族称为满三重组。对并运算封闭的满三重组称为满半AFL。对乘幂闭包封闭的满半 AFL称为满AFL。从一个语言族出发，经上述代数运算后得到的闭包分别称为由生成的满三重组、满半AFL和满AFL,以（）、()和（）表之。如果语言族只包含一个语言L，则由生成的结构分别称为满主三重组,满主半AFL及满主AFL。如果把同态限制为无空字同态,即不得把非空字映为空字，则所有以上定义中的“满”字皆应除去。

判别准则把非确定型有限自动机中的输出字母推广为输出字母串,所得的装置称为a转换器。把一个语言L的所有语句作输入,全体输出语句的集合即构成新语言L′。
一个语言族成为满三重组的充分必要条件是它在a转换器运算下是封闭的。对。又对K≥1构造任意的。在上定义同态h为：h(c)=ε,h(ɑ)=ɑ(对任意ɑ∈)，则L中任一语句S不会比它的映像h(s)长K倍以上。因此称h为K有界同态。所有的K有界同态统称有界同态。
一个语言族成为 AFL的充分必要条件是它在并运算、无空字乘幂闭包、无空字正则置换、与正则语言相交及有界同态下是封闭的。
一个语言族成为满 AFL的充分必要条件是它在并运算、乘幂闭包、正则置换、与正则语言相交及同态映射下是封闭的。
抽象接收器族 类似于从个别的语言到抽象语言族，从个别的自动机（接收器）出发也可得到相应的抽象接收器族，简称AFA。AFA接受语言族有两种方式。如果只要求该AFA最后进入终止状态,则接受的语言族正好是满半AFL。如果除了要求AFA进入终止状态外，还要求它的存储同时变空，则接受的语言族正好是满AFL。
乔姆斯基分层的四族语言0、1、2、3都是AFL,其中只有0、2、3是满AFL。1不是,因为它在一般的同态映射下不封闭。

正则语言正规语言又称正则语言是满足下述相互等价的一组条件的一类形式语言：

可以被确定有限状态自动机识别；

可以被非确定有限状态自动机识别；

可以被只读图灵机识别；

可以用正则表达式描述；

可以用正则文法生成。

可以用前缀文法生成。1

在字母表集合Σ上的正规语言定义如下：

空集合Ø是正规语言

只包含一个空字符串的语言{ε}是正规语言

对所有，{a}是正规语言

若A, B是正规语言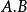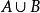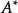，，，则都是正规语言1

除此之外都不是正规语言

如果一个语言不是正规语言，它需要一个内存至少是Ω(log log n)的自动机才能辨认。换句话说，DSPACE(o(log log n))等于所有正规语言的集合。实际上，大部分的非正规语言需要至少O(log n)的空间。

性质

正则语言的交、并、差、补运算得到的语言仍然是正则语言；

两个正则语言连接（把第一个语言的所有字符串同第二个语言的所有字符串连接起来）后得到的语言仍然是正则语言；

正则语言闭包运算后得到的语言仍然是正则语言；

正则语言的每个字符串转置后得到的语言仍然是正则语言；

正则语言被任意语言的字符串商（左商或右商)后得到的语言仍然是正则语言。

正则语言字符串代换后得到的语言仍然是正则语言。

与正则语言字符串同态或逆同态的语言仍然是正则语言。1

语言的抽象用代数方法描述程序设计语言, 能够使得程序设计语言具有清晰性、层次性和可操纵性, 是对研究程序设计语言之间的联系的一个有益尝试(提供语言的一个抽象模型)。具体的描述方法是: 用基调描述语言的抽象语法 , 一个基调 2= (S, F) 由它的类集 S(语言的基本语法元素)和操作集 F (语法元素间的组合关系)两部分组成。通过引进一组语义规则, 为基调2指定语义, 也即为基调 2 所对应的语言指定语义, 这样, 基调与引进的语义规则构成语言的一个抽象模型, 语言的这种抽象模型独立于一个语言的具体表示。2