球面被平面所截得的一部分叫做球冠。截得的圆叫做球冠的底,垂直于截面的直径被截得的一段叫做球冠的高。球冠也可以看成一段圆弧绕经过它的一个端点的直径旋转所成的曲面。球冠不是几何体,而是一种曲面。它是球面的一部分,是球面被一个平面截成的,球冠的任何部分都不能展开成平面图形。
公式球面被平面所截得的一部分叫做球冠。截得的圆叫做球冠的底,垂直于截面的直径被截得的一段叫做球冠的高。球冠也可以看成一段圆弧绕经过它的一个端点的直径旋转所成的曲面1。如图:
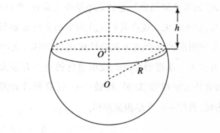
假设球面的半径是R,球冠的高是h,那么球冠的表面积公式为:
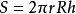
推导过程假定球冠最大开口部分圆的半径为 r ,对应球半径 R 有关系:r = Rcosθ,则有球冠积分表达:
球冠面积微分元 dS = 2πr×Rdθ = 2πR2×cosθ dθ
积分下限为θ,上限π/2
所以:S = 2πR×R(1 - sinθ)
其中:R(1 - sinθ)即为球冠的自身高度H
所以:S = 2πRH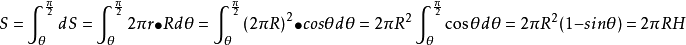
应用有了这个公式,我们就可以动手计算北回归线到北极的面积了。
由于北回归线位于北纬66°34’,地球半径尺= 6370km,我们要计算图中球冠的面积它的高:
h=O'N=R(1- sin66°34’)=525( km),代入球冠面积公式,
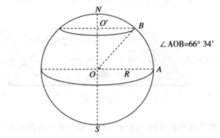 得S=2πRh =2π×6370×525 -21027584( km2)
得S=2πRh =2π×6370×525 -21027584( km2)
因而北回归线到北极的面积大约是21027584平方公里。
注意:球冠不是几何体,而是一种曲面。它是球面的一部分,是球面被一个平面截成的,球冠的任何部分都不能展开成平面图形,球冠的底面是圆而不是圆面,故球冠的面积不能包括底面圆的面积。球面被一个平面截成两个部分,这两个部分都是球冠,其中一个球冠的高小于球的半径,另一个球冠的高大于球的半径。前面介绍的球冠面积公式对其高小于、等于或大于球半径的球冠都适用,而球面积公式可看成球冠面积公式当h=2R的特例。
球缺的体积球缺:一个球被平面截下的一部分叫做球缺,截面叫做球缺的底面,垂直于截面的直径被截下的线段长叫做球缺的高2。
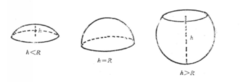
球缺是旋转体,它可由弓形绕着与弓形的弦垂直的直径旋转而得到。球缺也可以看做是球冠和球冠的底所在的圆面所围成的几何体。
我们在推导球的体积公式时,是先推导出一个特殊球缺——半球的体积,再2倍后得到的。对于一般的球缺,即h≠R时,它的体积公式的推导方法完全类似,只不过是把球的高R用一般球缺的高h去代替。所以当球的半径为R,球缺的高为h时,有
V球缺=V圆柱-V圆台=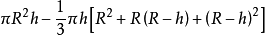
=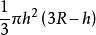
若球缺的高h′=2R-h,
∵hR。这时
V大球缺=V球-V小球缺
=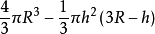
=
而把公式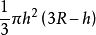 中的h换作
中的h换作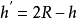 则得
则得
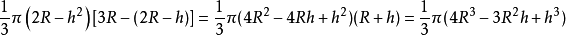
∴我们有以下定理:
**定理:**如果球的半径是R,球缺的高是h,那么球缺的体积是:3
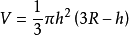
本词条内容贡献者为:
韩彦昌 - 教授 - 华南师范大学数学科学学院




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国