[科普中国]-黄金分割搜索-

基本概念

这里讨论的是在一个单峰函数搜索一个最小值（搜索一个最大值也一样），与找零不同，两个具有相反符号的求值函数足以包括一个根。当搜索最小值时，需要三个值。黄金分割搜索是逐步缩小定位最小值的有效方式。关键是要观察，无论有多少点已经被赋值，最小值在由与目前赋值最小的点相邻的两点所界定的区间内。

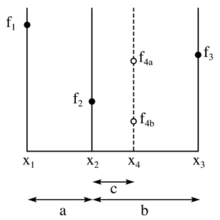
上图表示了算法中找最小值的一个步骤。f(x)的函数值位于垂直坐标轴上,参数x位于水平坐标轴。已经有三个位于函数f(x)上的点的值被计算出来。: x1, x2, 和x3。可见f2小于 f1和f3, 所以很明显的，最小值处于x1和x3之间。

接下来的步骤是通过计算函数位于另一个点x4的值。在最大的区间选择x4会更有效率，例如：x2和x3之间。从图中我们可以看出，如果函数的值落在f4a的话，最小值落于x1和x4之间，并且新的一组点将会是x1和x2和x4。然而如果函数的值为f4b的话，新的一组点将会是x2和x4和x3。因此，无论是哪种情况，我们都可以建立一个新的更狭窄的区间，用于搜索函数的最小值。

点的选择由图可知，新的区间会介于X1和X4，长度为a+c，或者介于X2和X3，长度为b。黄金分割搜索要求这些区间是相等的。若不是如此，较宽的区间会被使用很多次，降低了收敛率。为了确保b=a+c，算法应确保X4=X1-X2+X3。

然而X2的确定仍是一个问题。我们避免了X2非常接近X1或者X3的情况，确保了每一次迭代区间宽度会缩小同样的比例。

为了确保计算f(X4)后的值与之间的成比例，假设f(X4)的值为f4a，且我们新的一组点为X1,X2和X4，则必须使：

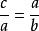。然而，如果f(X4)的值为f4b ，并且我们新的一组点为X2，X4和X3，则必须使：

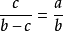。结合b=a+c可解得

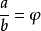
而φ就是黄金比例：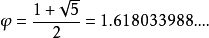

这就是这个算法被成为黄金分割搜索的原因。1

终止条件由于平滑的函数是平稳的（它们的一阶导数接近于零）接近于最小值，所以必须注意不要太高的定位精度，在书>> f = lambda x: (x-2)**2

>>> x = gss(f, 1, 5)

>>> x

2.000009644875678

'''

c = b - (b - a) / gr

d = a + (b - a) / gr

while abs(c - d) > tol:

if f(c)

b = d

else:

a = c

# we recompute both c and d here toavoid loss of precision which may lead to incorrect results or infinite loop

c = b - (b - a) / gr

d = a + (b - a) / gr

return (b + a) / 2

递归

public static double PHI = (1 +Math.sqrt(5)) / 2; // 0.618...

public static double RESPHI = 2 - PHI; // 0.382...

/**

* Golden section search.

* @param x1The left bound of current bounds.

* @param x2An interior point between (x1, x3).

* @param x3The right bound of current bounds.

* @param tau The error tolerance to judgethe convergence, recommended value is e^0.5, where e is is the requiredabsolute precision of f(x).

public double goldenSectionSearch(doublex1, double x2, double x3, double tau) {

double x4;

if (x3 - x2 > x2 - x1) { // b > a，右半区间长度较大

x4 = x2 + RESPHI * (x3 - x2); // x4安插在右半区间

} else {// b a，右半区间长度较大

return goldenSectionSearch(x2, x4, x3,tau); // 以x2，x4，x3作为新三点，继续搜索

} else {// b x2 - x1) { // b > a，右半区间长度较大

return goldenSectionSearch(x1, x2, x4,tau); // 以x1，x2，x4作为新三点，继续搜索

} else {// b =2）。该数列越往后相邻的两个数的比值越趋向于黄金比例值（0.618）。

斐波那契查找就是在二分查找的基础上根据斐波那契数列进行分割的。在斐波那契数列找一个等于略大于查找表中元素个数的数F[n]，将原查找表扩展为长度为F[n](如果要补充元素，则补充重复最后一个元素，直到满足F[n]个元素)，完成后进行斐波那契分割，即F[n]个元素分割为前半部分F[n-1]个元素，后半部分F[n-2]个元素，找出要查找的元素在那一部分并递归，直到找到。

斐波那契查找的时间复杂度还是O(log 2 n )，但是与折半查找相比，斐波那契查找的优点是它只涉及加法和减法运算，而不用除法，而除法比加减法要占用更多的时间，因此，斐波那契查找的运行时间理论上比折半查找小，但是还是得视具体情况而定。

对于斐波那契数列：1、1、2、3、5、8、13、21、34、55、89……（也可以从0开始），前后两个数字的比值随着数列的增加，越来越接近黄金比值0.618。比如这里的89，把它想象成整个有序表的元素个数，而89是由前面的两个斐波那契数34和55相加之后的和，也就是说把元素个数为89的有序表分成由前55个数据元素组成的前半段和由后34个数据元素组成的后半段，那么前半段元素个数和整个有序表长度的比值就接近黄金比值0.618，假如要查找的元素在前半段，那么继续按照斐波那契数列来看，55 = 34 + 21，所以继续把前半段分成前34个数据元素的前半段和后21个元素的后半段，继续查找，如此反复，直到查找成功或失败，这样就把斐波那契数列应用到查找算法中了。