[科普中国]-密克定理

密克定理是几何学中关于相交圆的定理。1838年，奥古斯特·密克（Auguste Miquel）叙述并证明了数条相关定理。许多有用的定理可由其推出1。密克的第一条定理，是十八世纪已有的著名经典结果。

定义密克定理是几何学中关于相交圆的定理。1838年，奥古斯特·密克（Auguste Miquel）叙述并证明了数条相关定理。许多有用的定理可由其推出。

定理：设在一个三角形的每一边上取一点，过三角形的每一顶点与两条邻边上所取的点作圆，则这三个圆共点2。利用圆周角性质易证此定理3。

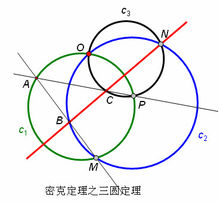
定理陈述三圆定理设三个圆C1, C2, C3交于一点O，而M, N, P分别是C1 和C2, C2和C3, C3和C1的另一交点。设A为C1的点，直线MA交C2于B，直线PA交C3于C。那么B, N, C这三点共线。（注意：M、N、P并不共线）

证明思路：

1、圆C2和C3用圆幂定理，再套到C1里，化简得梅涅劳斯等式。

2、连几条线，三个四点共圆导角得到三点共线（三圆共点的条件可以转换成三条公共弦的三线共点）。

3、先画两个圆，假设点N是BC延长线与圆c2的交点，再导角证明OCPN共圆。

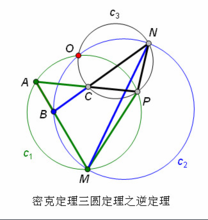
逆定理：如果是三角形，M, N, P三点分别在边AB, BC, CA上，那么△AMP、△BMN、△CPN 的外接圆交于一点O。

完全四线形定理如果ABCDEF是完全四边形，那么三角形的外接圆交于一点 O，称为密克点。

四圆定理设C1, C2,C3, C4为四个圆，A1和B1是C1和C2的交点，A2和B2是C2 和C3的交点，A3和B3是C3和C4的交点，A4和B4是C1和C4的交点。那么A1, A2, A3, A4四点共圆当且仅当B1, B2, B3, B4四点共圆。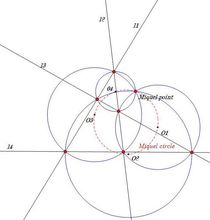

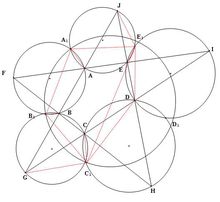
五圆定理设ABCDE为任意五边形，五点F, G, H, I, J分别是EA和BC , AB和CD, BC和DE, CD和EA, DE和AB的交点，那么三角形的外接圆的五个不在五边形上的交点共圆，不穿过这些交点的圆也穿过五个外接圆的圆心。

发展简史1838年奥古斯特·密克在约瑟夫·刘维尔的期刊《Journal de mathématiques pures et appliquées》（纯粹与应用数学杂志）发表了这定理的一部份。

密克的第一条定理，是十八世纪已有的著名经典结果，以圆周角定理证明。

完全四线形四圆的交点称为密克点，但这性质雅各布·施泰纳在1828年已经知道，威廉·华莱士也已经知道。

五圆定理是一条更一般的定理的特殊情形。这条定理由威廉·金登·克利福德提出及证明。2000年12月20日，江泽民主席出席澳门回归祖国一周年庆典活动期间，在参观濠江中学时向该校师生出了一道求证“五点共圆”的问题，令问题重新引起广泛兴趣。阿兰·科纳在2002年10月的一个研讨会也重提这问题。

本词条内容贡献者为:

郎奠波 - 副教授 - 黑龙江财经学院