[科普中国]-卷积积分

卷积与傅里叶变换有着密切的关系。以(x) ，(x)表示L1（R）1中f和g的傅里叶变换，那么有如下的关系成立：（f *g）∧（x）=(x)·(x)，即两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换。这个关系，使傅里叶分析中许多问题的处理得到简化。

由卷积得到的函数（f *g）（x），一般要比f，g都光滑。特别当g为具有紧支集的光滑函数，f 为局部可积时，它们的卷积（f *g）（x）也是光滑函数。利用这一性质，对于任意的可积函数 ， 都可以简单地构造出一列逼近于f 的光滑函数列fs（x），这种方法称为函数的光滑化或正则化。

卷积的概念还可以推广到数列 、测度以及广义函数上去。

学习1信号与系统必须贯穿一个核心的思想，那就是信号分解的思想 。看到一个很复杂的信号，我们往往是无从下手的，这个时候若能把复杂的信号进行分解，分解成我们常见的信号，复杂信号的分析过程自然就演变成了对简单信号的分析 。也就是说我们只需要掌握一些比较典型的简单信号的特性，而刚好一些复杂的信号都可以表示成这些简单信号的组合，那么我们就可以实现复杂信号的分析，卷积积分的思想就源自于此。

那么到底什么样的简单信号可以表示复杂信号呢？其实如果这个问题能够回答好的，信号与系统的核心问题就解决了 。对时域而言，对于连续信号，单位冲激信号就可以实现这样的功能，于是通过推导和演变，就引出了卷积积分的定义式 。在频域，是把复杂的信号表示成不同频率的正弦信号的线性组合，于是就引出了信号的傅里叶变换，离散信号同样如此。

任意连续信号可以分解成单位冲激信号的线性组合， 也就是说任意连续信号都可以分解成不同强度的冲激信号的线性叠加，对于不同的信号而言，分解的形式都是相同的，不同仅仅是 f(τ)这样的一个积分形式即定义为卷积积分。

任何信号1都可以表示成信号本身和单位冲激信号的卷积，展开就是卷积积分的形式，不同的信号都可以分解成相同的形式，那么这个过程就简化了分析。 另外，当分析信号作用系统的响应时，对于任意信号作用于某个冲激响应为 的LTI系统而言，利用叠加性和均匀性就可以得到其输出的零状态响应。最后可以得到的结论是系统的零状态响应是输入信号和系统的单位冲激响应的卷积积分 。利用这样的一种卷积积分的方法来求系统的零状态响应较之经典的时域分析法要简单很多，而且物理含义也比较明确。

在激励条件下，线性电路在t时刻的零状态响应=从激励函数开始作用的时刻（ξ=0）

到t时刻（ ξ=t）的区间内，无穷多个强度不同的冲激响应的总和。

可见，冲激响应在卷积中占据核心地位。

卷积积分2在时域分析中是一个很重要的概念和数学工具。除了卷积的图解法和数值解以外 ，直接根据卷积定义的函数式求积分也可以采用几种不同的方来进行 。

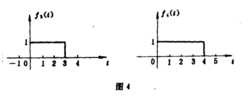
现以图1 所示两个波形为例, 用下述不同方法求解f(t) *g(t)。

求2上列两函数的卷积时,可分为图2 所求5个区间来进行。

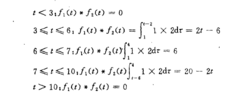
用此法进行卷积积分,数学概食清楚,函数计算式简单,借助于一定的图形,卷积的物理含义亦十分清晰。在每段时间域中f1(t)*f2(t)与t的函数关系一目了然。它适用于任何两个信号的卷积积分计算。间题就是对初学者积分的上、下限不易正确确定。通常,在每个分段时间域中,若函数f1( )和f2(t- )两波形的后沿值(即函数不为零的最小值)分别为tr1和tr2,两波形前沿值(即函数右边界

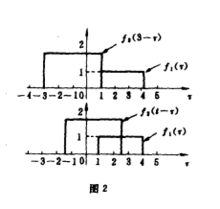
的最大r值)分别为tr1和tr2,则积分的下限应取它们后沿值中的最大者,即max〔tr1,tr2〕,积分上限取它们前沿值中的最小者,即min〔tr1,tr2〕。

可将2上列函数分别表示为

f1(t)=v(t-1)-v(t-4)

f2(t)=2[v(t-2)-v(t-6)]

由此得:

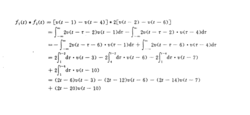
这种种卷积方法用一个函数表达式可将结果全部表示出来,且根据各个积分的被积函数v(t- -t1)·v( 一t0)所确定的门限,很容易将门的上、下限分别确定为积分的上限(t一t1)、下限(t0),积分后各函数的定义域的下限只要由积分的上限减去下限(t一t1一t0)后即可确定。因此该方法容易理解和掌握,尤其对初学者很容易接受。它除了适用厂于上列分段函数的卷积分外,还可适用于连续函数波形。

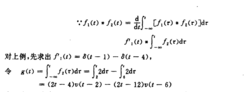
由于2冲激函数与任何函数的卷积积分皆为该函数本身,因此很快可求出

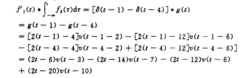
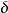
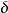
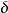用该性质求卷积,可避免复杂的积分运算,同时也避免了确定积分限的问题,它非常适合于两函数中一个为阶跃信号或斜坡信号或可用阶跃信号的组合来表示的折线信号,由于u'(t)= 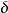(t)(或[tv(t)])”=(t)而f(t)*(t)=f(t),由此计算自然会简化一些.但是该方法的应用有一定的限制,它必须要求f1(- 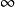)=f2(- 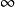)=0.另外,如果不合理地乱加应用,比如对一信号求导,而对另一信号的积分并不容易,则使得整个计算并不简单,或许还会计算出错误的结果.

设2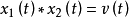

则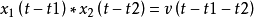

用此性质,可将上列两波形先移至如图4所示的位里,分别用f3(t)和f4(t)来表示:

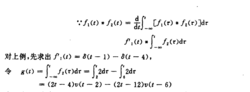
再由卷积的线性性：

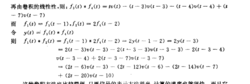
这种卷积方法也比较简便,只要信号的表示方法得当,计算的速度也就很快。而且它

对连续函数亦适用。

上面对同一例题,用4种不同方法对卷积积分进行了计算。这些常用方法对我们在信号与系统课程中所遇到的绝大部分信号的卷积计算都是适用的(除参予卷积的两信号中有一为冲激信号,可直接进行计算,不必再用2、3、4方法)。通过比较还可知,分段卷积法最直接明了,但其它三种方法都比较容易接受和掌握。

在3电路分析中要求解任意激励的零状态响应时，可采用卷积积分法和拉普拉斯变换法，现分别叙述如下：（1）卷积积分法已知电路的冲激响应为h（t），则任意激励e（t）的零状态响应r（t）求得拉普拉斯变换法（也称运算法）①先将表示电压或电流的时域形式的任意激励f（）做拉氏变换，得到复频域的电压或电流激励的象②从等效运算电路求解以象函数为变量的线性代数方程，得到电压或电流响应的象函数。③再利用拉氏反变换（通常可以查表）求原函数，即可得任意激励e（t）的时域形式的零状态响应。

在4电路分析中,应用卷积积分时,首先要找到单位冲激响应,这是在电路分析中正确应用卷积积分的关键所在,而单位冲激响应可以通过网络函数的反拉氏变换求得.一般对应的网络函数求解较为方便。那么给定的任何激励的零状态响应都可以通过卷积积分求得.如果网络处于非零状态,则全响应把上叙结果加上零输入响应即为所求.