[科普中国]-符号函数

定义

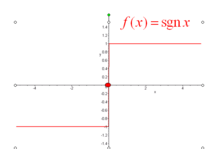
符号函数（signum）可由阶跃信号得来。对于符号函数在跳变点可以不予定义，或规定sgn（0）=0。

显然，可以用阶跃信号来表示符号函数：

sgn（x）=2u（t）-1

即 x>0,sgnx=1

x=0,sgnx= 0

x 0]任何实数都可以表示为其绝对值和符号函数的积：

x= (sgn x) | x|若x不为零，可以由上式得出符号函数的另一个定义：

sgn(x)=x/|x|

符号函数是绝对值函数的导数：

d|x|/dx=x/|x| 除了在0，符号函数可微分，其导数为0。透过一般化微分概念，可以说符号函数是狄拉克δ函数的两倍：

dsgn(x)/dx=2δ（x） 它和单位步阶函数的关系：

sgn x= 2H1 / 2(x) − 1

特性其定义域为R，值域为{-1,0,1}；

2.有唯一的跳跃间断点x=0;

3.单调性：它是不严格递增的非周期函数；

4.奇偶性：由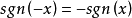 可知它在定义域R内是奇函数；

5.可导性：它在非原点处都可导，且导数为0；

6.它在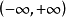上没有原函数；

7.它在任意区间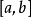 上都Rieman可积;

8.。

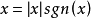应用可用于说明可积函数不一定存在原函数

由于x=0是y=sgn(x)的唯一跳跃间断点，故在任何以x=0为内点的区间上，sgn(x)不存在原函数。而在任

何以闭区间[a,b]上Rieman可积，且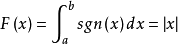 ，在x=0处 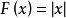不可导，F(x)并不是

y=sgn(x)的原函数，说明可积函数不一定存在原函数，有助于弄清楚函数的Rieman可积与存在原函数之间互

不蕴含的关系，还可以作为原函数存在定理中条件f(x)在[a,b]上连续不满足时，结论不成立的反例，强调条件

不可缺少而引起重视2。

2.用于简化带绝对值函数积分的计算

对含有绝对值的函数 ,可先把绝对值去掉化为分段函数求解 ,也可以用一种更为简单的求解方法 ,就是引入

符号函数来简化积分的运算。

例:

符号函数在积分过程中可视为常数系数，是解题过程简化。因此对于一些含有绝对值的函数可用此法解决。