[科普中国]-双边拉普拉斯变换

定义

若ƒ(t)为实数t的实数函数或是复变函数，t可以为任意实数，则双边拉普拉斯变换可以用以下的积分表示：

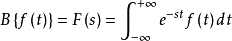
此积分为反常积分，此积分收敛当且仅当以下二个积分都存在：

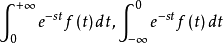
上述F(s)在s的的某一区域内收敛（即小于无穷大），则由此积分确定的函数称为f(t)的双边拉普拉斯变换，或称为f(t)的象函数1。而称f(t)为F(s)的原函数。

使得F(s)收敛的s的取值范围称为拉氏变换的收敛域。

注：在给出某函数的双边拉氏变换时必须注明其收敛域。

优点信号不必限制在范围t>0内，在某些情况下把所研究的问题从时间负无穷到正无穷上作统一考虑，可使概念更清楚。

双边拉氏变换与傅里叶变换的联系密切，便于全面理解傅氏变换，拉氏变换及Z变换的关系。

与傅氏变换的关系f(t)的双边拉普拉斯变换其实就是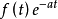 的傅氏变换。如果双边拉普拉斯变换式的收敛域包括虚轴在内，则把F(s)中的s代换成jw就得到f(t)的傅氏变换，即有：

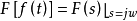故可以把傅氏变换看成双边拉氏变换的特例，或双边拉氏变换是傅氏变换的推广1。

性质1.线性。

若有：,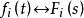

其收敛域为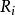

则有：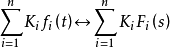

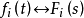
其中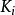为常数，可为实数也可为复数，收敛域R一般取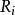的重叠部分，也有可能扩大，若无重叠部分，此性质不成立。该性质利用拉氏正变换性质即可得2。

2.延时(时移特性)

若有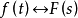：则有：

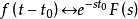其中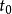 可正可负，收敛域不变2。

3.s域平移

若有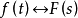,其收敛域为R，则有：

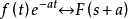其收敛域为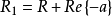 ，其中Re{-a}表示取-a的实部2。