[科普中国]-终值定理

连续系统中终值定理定理内容

连续系统的拉普拉斯变换对应的终值定理如下所示：

设有连续函数f(t)，当t趋于无穷时，f(t)的极限存在，且有：

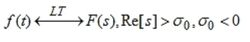
则终值定理可表达为：

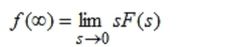
该定理说明了，当满足一定使用条件时，可由S域的象函数直接得到时域连续函数的终值。

注意：终值定理是取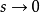 的极限，因而s=0的点应在sF(s)的收敛域内，否则不能应用终值定理。

典例如函数f(t)的象函数 ， 。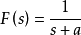

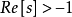求原函数f(t)的初值和终值。

解：（1）由初值定理，得： ；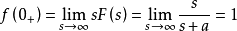

由F(s)的原函数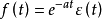 ，显然以上结果对a>0或a0，则有 ；

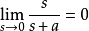② 若a=0，则有 ；

③若a