若在整个数轴上
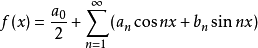 且等式右边级数一致收敛,则有如下关系式:1
且等式右边级数一致收敛,则有如下关系式:1
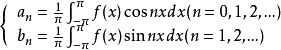
一般地说,若 是以
是以 为周期且在
为周期且在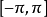 上可积的函数 ,则按上式计算出的
上可积的函数 ,则按上式计算出的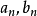 称为函数
称为函数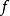 (关于三角函数系)的傅里叶系数,以
(关于三角函数系)的傅里叶系数,以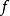 的傅里叶系数为系数的三角级数称为
的傅里叶系数为系数的三角级数称为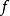 (关于三角函数系)的傅里叶级数,记作:
(关于三角函数系)的傅里叶级数,记作:
其中,记号“ ”表示上式右边是左边函数的傅里叶级数1
”表示上式右边是左边函数的傅里叶级数1
若 是以
是以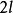 为周期且在
为周期且在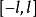 上可积的函数 ,则:
上可积的函数 ,则:
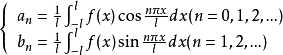
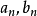 称为函数
称为函数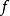 (关于三角函数系)的傅里叶系数1
(关于三角函数系)的傅里叶系数1
若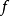 是以
是以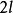 为周期的偶函数,或是定义在
为周期的偶函数,或是定义在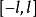 上的偶函数 ,则:
上的偶函数 ,则:
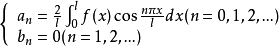
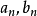 称为函数
称为函数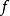 (关于三角函数系)的傅里叶系数1
(关于三角函数系)的傅里叶系数1
若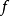 是以
是以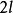 为周期的奇函数,或是定义在
为周期的奇函数,或是定义在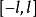 上的奇函数 ,则:
上的奇函数 ,则:
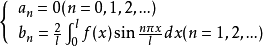
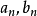 称为函数
称为函数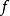 (关于三角函数系)的傅里叶系数1
(关于三角函数系)的傅里叶系数1
定理1
(贝塞尔不等式)
若函数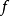 在
在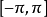 上可积,则
上可积,则
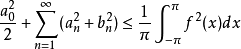
其中,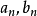 为函数
为函数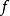 的傅里叶系数1
的傅里叶系数1
定理2
若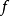 是以
是以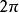 为周期且在
为周期且在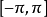 上可积的函数 ,则它的傅里叶级数部分和
上可积的函数 ,则它的傅里叶级数部分和
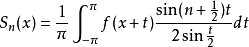 当
当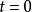 时,被积函数中的不定式由极限
时,被积函数中的不定式由极限
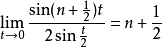
来确定。1
信号与系统三角傅里叶级数以高等数学中的知识,任何周期为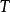 的周期函数
的周期函数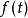 ,在满足狄利克雷条件时,可以由三角函数的线性组合来表示
,在满足狄利克雷条件时,可以由三角函数的线性组合来表示
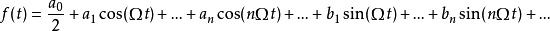 上式即为周期信号的三角傅里叶级数表达式,其中,
上式即为周期信号的三角傅里叶级数表达式,其中,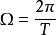 为基波信号,
为基波信号,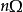 为
为 次谐波频率,
次谐波频率,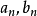 是傅里叶系数。
是傅里叶系数。
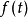 又可表示为
又可表示为
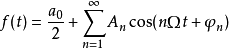 其中,傅里叶系数
其中,傅里叶系数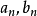 ,振幅
,振幅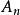 ,相位
,相位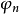 之间的关系是
之间的关系是
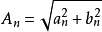
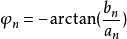
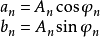 可看出,
可看出,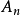 和
和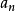 都是
都是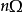 的偶函数,
的偶函数,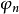 和
和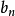 都是
都是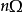 的奇函数2。
的奇函数2。
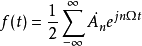
其中,傅里叶系数

还可写成2:
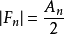




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国